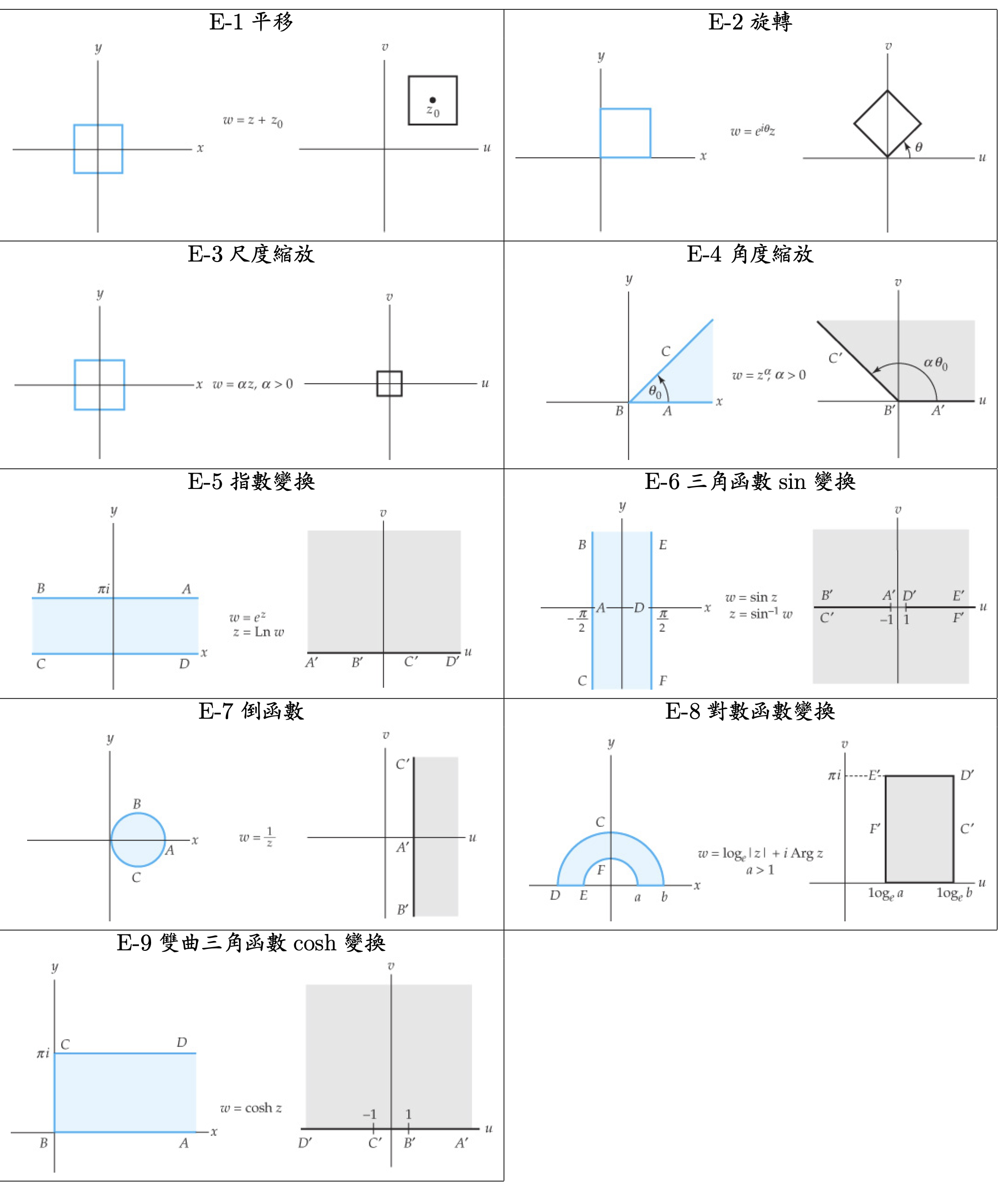
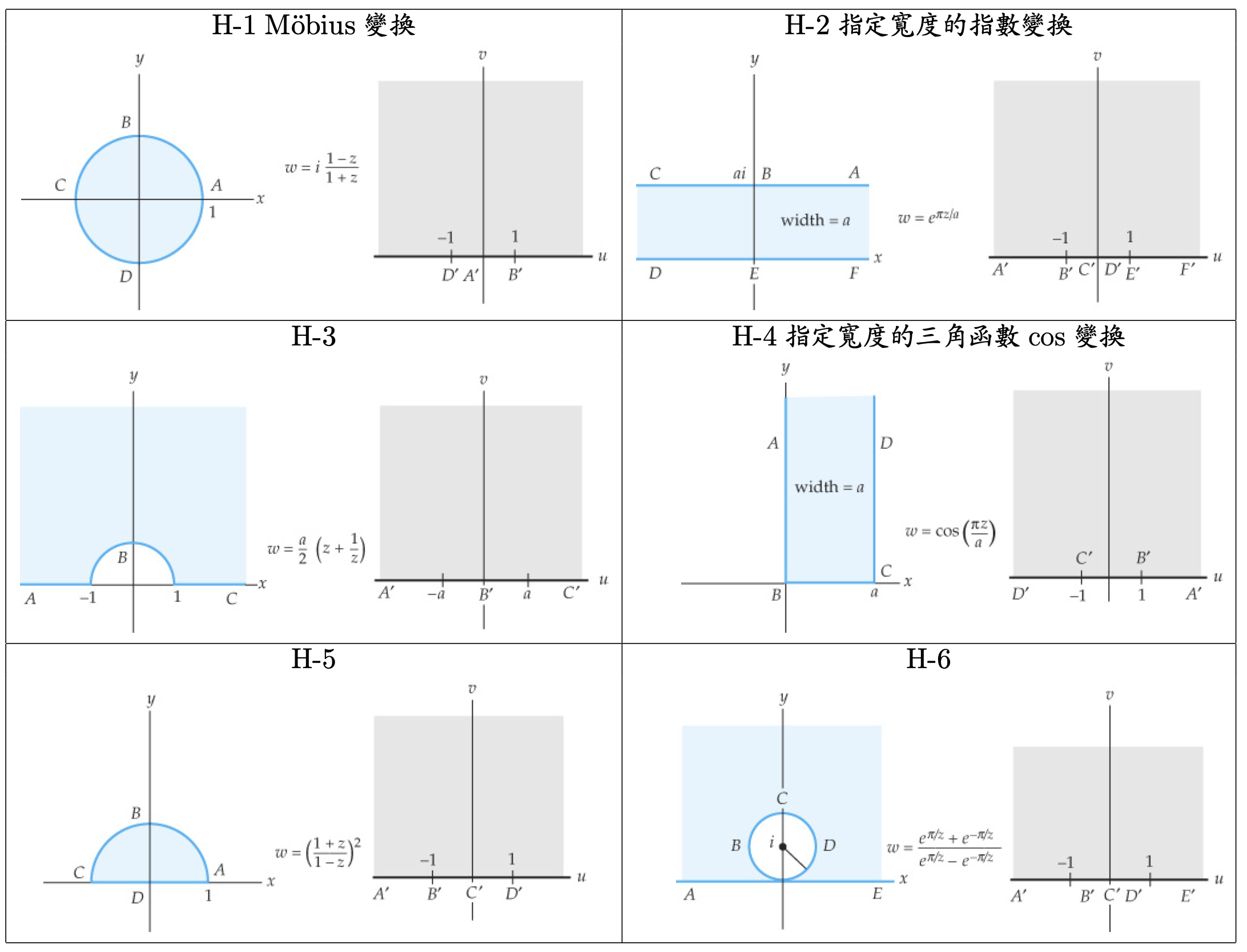
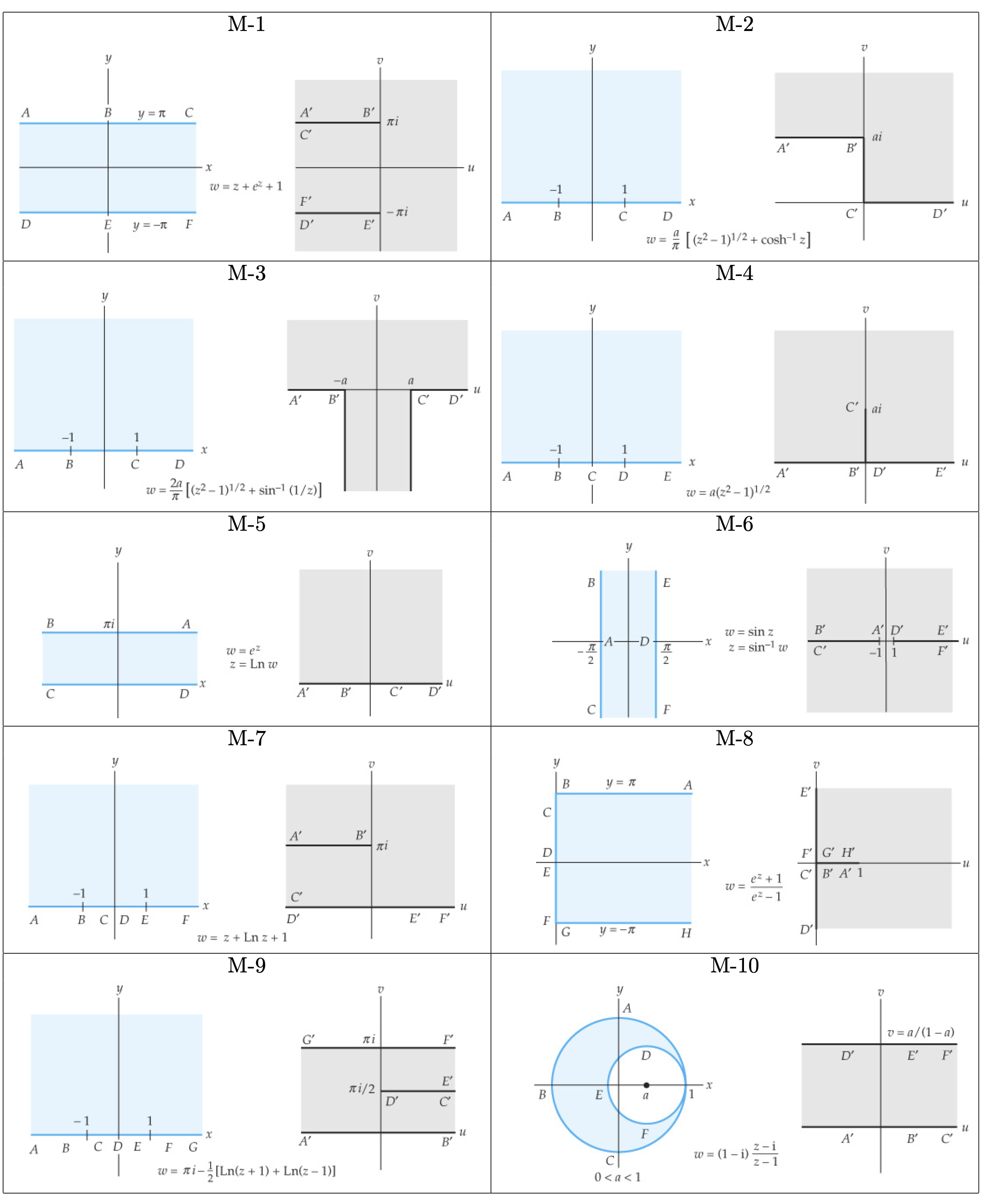
Schwarz-Christoffel 變換
此種變換主要的目的便是將上半平面對應的多邊形的區域。Schwarz-Christoffel變換是複分析中的一種映射,將上半平面映射到多邊形。這種變換由Hermann A. Schwarz ((1843–1921) 和 Elwin B. Christoffel (1829–1900) 兩位數學家獨立發現。Schwarz-Christoffel變換能夠將上半平面的實軸(無窮遠處除外)映射到多邊形的各邊,並且保持角度不變。因此,這種變換在複變數函數的積分計算和物理問題的求解中有著廣泛的應用。
進入主題之前,先行回顧在保角變換 w = f ( z ) w=f(z) w = f ( z ) z = z 0 z=z_0 z = z 0 C \mathcal{C} C z ( t ) = x ( t ) + i y ( t ) z(t)=x(t)+ i y(t) z ( t ) = x ( t ) + i y ( t ) t ∈ [ a , b ] t\in[a,b] t ∈ [ a , b ] C \mathcal{C} C z 0 = z ( t 0 ) z_0=z(t_0) z 0 = z ( t 0 )
τ = z ′ ( t 0 ) = x ′ ( t 0 ) + i y ( t 0 ) . \tau = z'(t_0)=x'(t_0)+ i y(t_0). τ = z ′ ( t 0 ) = x ′ ( t 0 ) + i y ( t 0 ) . 曲線 C \mathcal{C} C w = f ( z ) w=f(z) w = f ( z ) K \mathcal{K} K
w = u ( x ( t ) , y ( t ) ) + i v ( x ( t ) , y ( t ) ) , t ∈ [ a , b ] , w=u(x(t),y(t))+ i v(x(t),y(t)),\quad t\in[a,b], w = u ( x ( t ) , y ( t )) + i v ( x ( t ) , y ( t )) , t ∈ [ a , b ] , 來表示,同時 K \mathcal{K} K w 0 = f ( z 0 ) w_0=f(z_0) w 0 = f ( z 0 )
T = w ′ ( z 0 ) = f ( z 0 ) z ′ ( t ) . \mathbf{T}=w'(z_0)= f(z_0)z'(t). T = w ′ ( z 0 ) = f ( z 0 ) z ′ ( t ) . 設 τ \tau τ β = Arg z ′ ( t ) \beta=\text{Arg}~z'(t) β = Arg z ′ ( t ) T \mathbf{T} T
Arg T = Arg [ f ′ ( z 0 ) z ′ ( t 0 ) ] = Arg f ′ ( z 0 ) + β . \text{Arg}~\textbf{T}=\text{Arg}[f'(z_0)z'(t_0)]=\text{Arg}~f'(z_0)+\beta. Arg T = Arg [ f ′ ( z 0 ) z ′ ( t 0 )] = Arg f ′ ( z 0 ) + β . 亦即將曲線 C \mathcal{C} C z 0 z_0 z 0 τ \tau τ Arg f ′ ( z 0 ) \text{Arg}~f'(z_0) Arg f ′ ( z 0 ) K = f ( C ) \mathcal{K}=f(\mathcal{C}) K = f ( C ) w 0 = f ( z 0 ) w_0=f(z_0) w 0 = f ( z 0 )
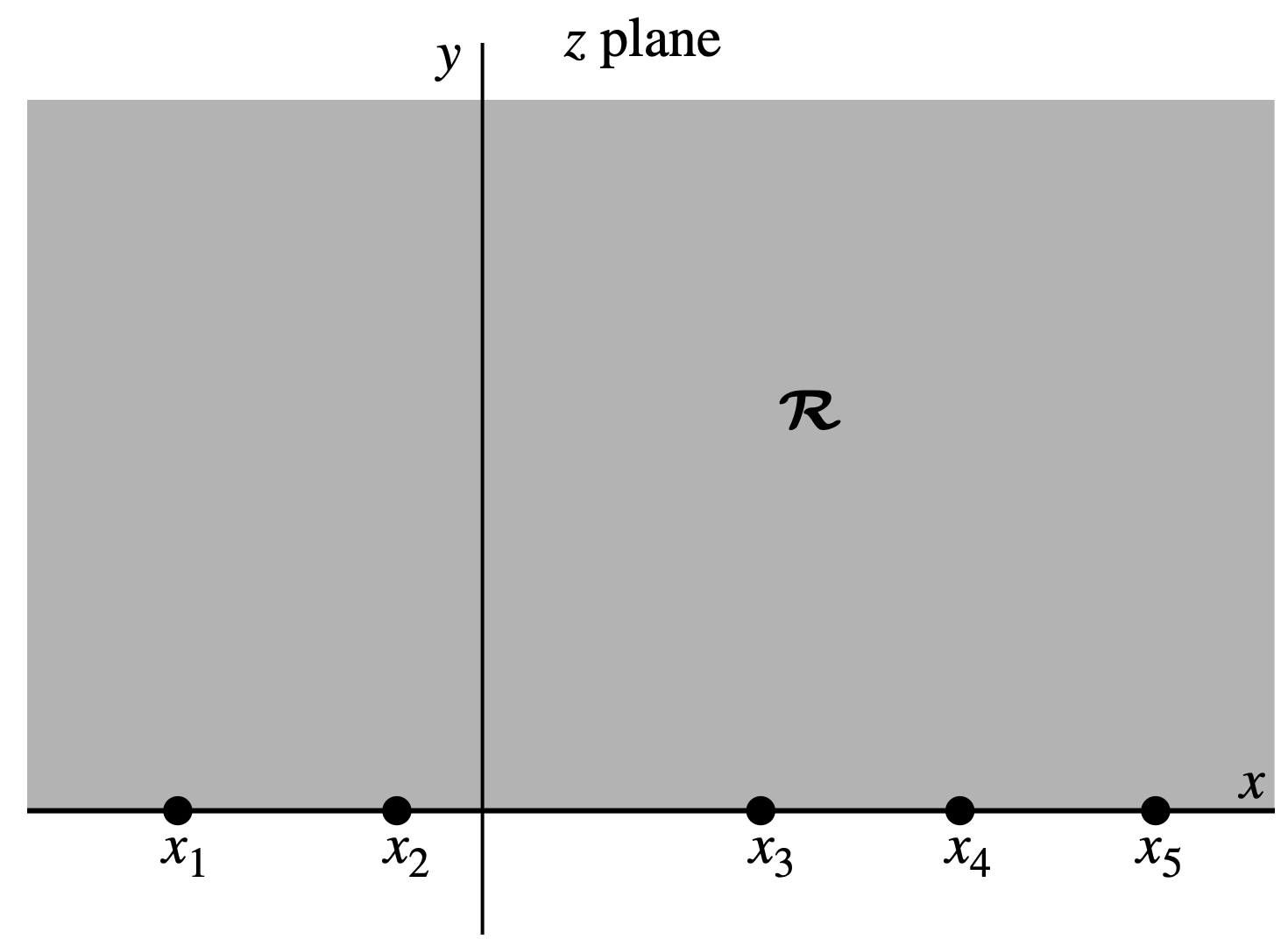
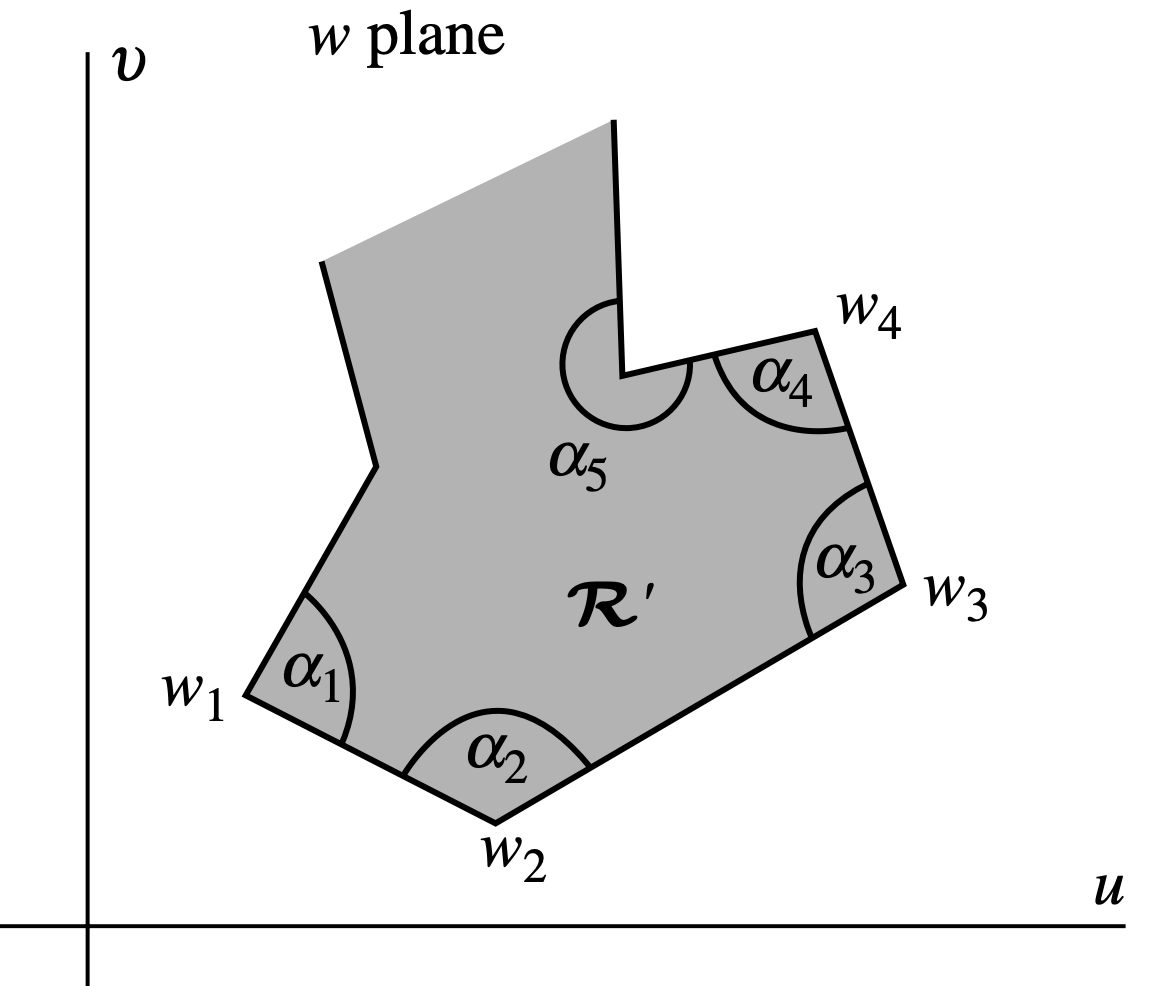
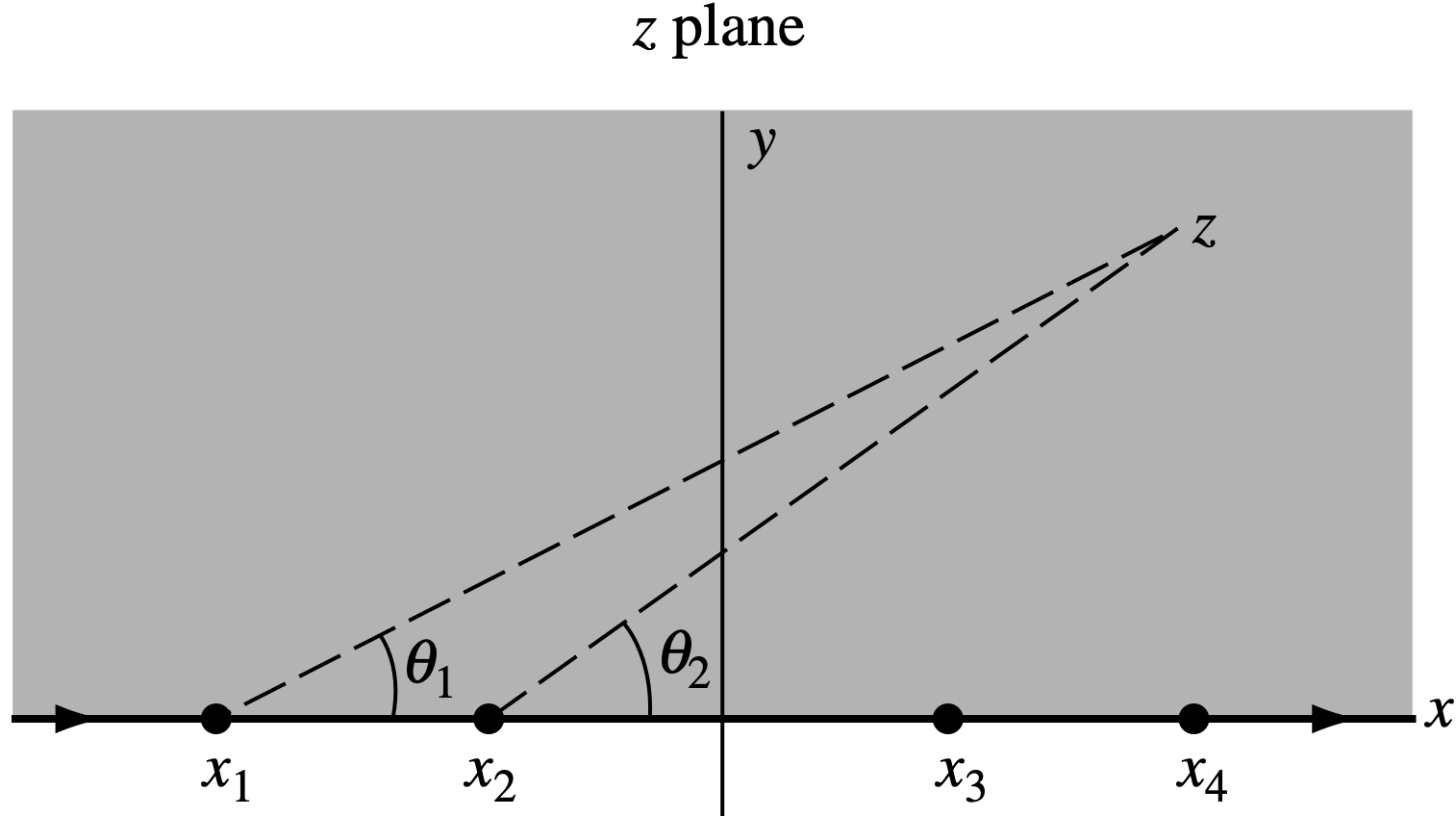
由於許多應用保角變換所相關的問題的定義域在 z z z R \mathcal{R} R w w w R ′ \mathcal{R}' R ′ R ′ \mathcal{R}' R ′ w w w P \mathcal{P} P w 1 , w 2 , … , w n w_1,~w_2,\ldots,~w_n w 1 , w 2 , … , w n α 1 , α 2 , … , α n \alpha_1,~\alpha_2,\ldots,~\alpha_n α 1 , α 2 , … , α n w 1 , w 2 , … , w n w_1,~w_2,\ldots,~w_n w 1 , w 2 , … , w n z z z x 1 , x 2 , … , x n x_1,~x_2,\ldots,~x_n x 1 , x 2 , … , x n w = f ( z ) w=f(z) w = f ( z )
w k = f ( x k ) , k = 1 , 2 , … , n . (9.3-1) w_k=f(x_k),\quad k=1,2,\ldots,n.\tag{9.3-1} w k = f ( x k ) , k = 1 , 2 , … , n . ( 9.3-1 ) 因此此保角變換將z z z x x x w w w P \mathcal{P} P z z z R \mathcal{R} R P \mathcal{P} P R ′ \mathcal{R}' R ′
如此一來,從 z z z
d w d z = A ( z − x 1 ) α 1 / π − 1 ( z − x 2 ) α 2 / π − 1 ⋯ ( z − x n ) α n / π − 1 , (9.3-2) \frac{dw}{dz}
=A (z-x_1)^{\alpha_1/\pi-1}
(z-x_2)^{\alpha_2/\pi-1}
\cdots
(z-x_n)^{\alpha_n/\pi-1}, \tag{9.3-2} d z d w = A ( z − x 1 ) α 1 / π − 1 ( z − x 2 ) α 2 / π − 1 ⋯ ( z − x n ) α n / π − 1 , ( 9.3-2 ) 積分可得 Schwarz-Christoffel 變換的一般形式是:
w = f ( z ) = A ∫ 0 z ∏ k = 1 n ( ζ − x k ) α k / π − 1 d ζ + B , (9.3-3) w = f(z) = A \int_0^z \prod_{k=1}^n (\zeta - x_k)^{\alpha_k/\pi-1} d\zeta + B, \tag{9.3-3} w = f ( z ) = A ∫ 0 z k = 1 ∏ n ( ζ − x k ) α k / π − 1 d ζ + B , ( 9.3-3 ) 其中A A A B B B x n x_n x n ∞ \infty ∞
w k = f ( x k ) , k = 1 , 2 , … , n − 1 , w n = f ( ∞ ) , x 1 < x 2 < ⋯ < x n − 1 < ∞ . \begin{align*}
w_k=f(x_k),&\quad k=1,2,\ldots,n-1, \\
w_n = f(\infty),&\quad x_1<x_2<\cdots<x_{n-1}<\infty.
\end{align*} w k = f ( x k ) , w n = f ( ∞ ) , k = 1 , 2 , … , n − 1 , x 1 < x 2 < ⋯ < x n − 1 < ∞.
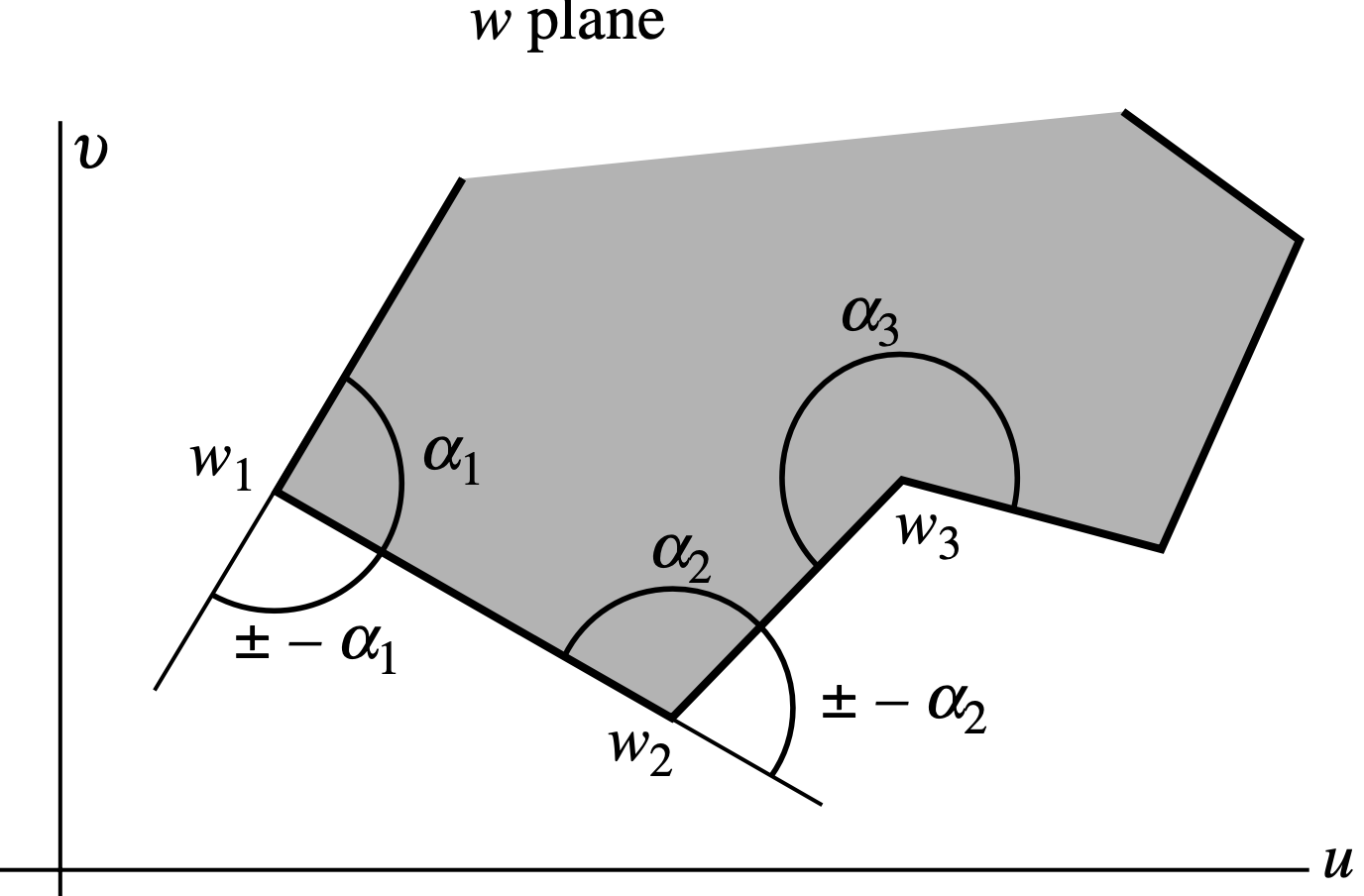
參考下圖,由(9.3-2)式知
arg d w = arg d z + arg A + ( α 1 π − 1 ) arg ( z − x 1 ) + ( α 2 π − 1 ) arg ( z − x 2 ) + ⋯ + ( α n π − 1 ) arg ( z − x n ) , \begin{align*}
\arg dw &= \arg dz+\arg A+\left(\frac{\alpha_1}{\pi}-1\right)\arg(z-x_1)+ \left(\frac{\alpha_2}{\pi}-1\right)\arg(z-x_2) \\
&\quad+\cdots+\left(\frac{\alpha_n}{\pi}-1\right)\arg(z-x_n), \tag{9.3-4}
\end{align*} arg d w = arg d z + arg A + ( π α 1 − 1 ) arg ( z − x 1 ) + ( π α 2 − 1 ) arg ( z − x 2 ) + ⋯ + ( π α n − 1 ) arg ( z − x n ) , ( 9.3-4 ) 當 z z z x 1 x_1 x 1 x 1 x_1 x 1 w w w w 1 w_1 w 1 z z z z z z x 1 x_1 x 1 θ = arg ( z − x 1 ) \theta=\arg (z-x_1) θ = arg ( z − x 1 ) π \pi π 0 0 0 arg d w \arg dw arg d w ( α 1 / π − 1 ) arg ( z − x 1 ) = ( α 1 / π − 1 ) π = α 1 − π (\alpha_1/\pi -1)\arg(z-x_1)=(\alpha_1/\pi -1)\pi=\alpha_1-\pi ( α 1 / π − 1 ) arg ( z − x 1 ) = ( α 1 / π − 1 ) π = α 1 − π π − α 1 \pi-\alpha_1 π − α 1 w 1 w_1 w 1 π − α 1 \pi-\alpha_1 π − α 1 w 1 w 2 w_1 w_2 w 1 w 2
同樣地,當 z z z x 2 x_2 x 2 x 2 x_2 x 2 arg ( z − x 1 ) \arg(z-x_1) arg ( z − x 1 ) arg ( z − x 2 ) \arg(z-x_2) arg ( z − x 2 ) π − α 2 \pi-\alpha_2 π − α 2 w w w w 2 w_2 w 2 π − α 2 \pi-\alpha_2 π − α 2 w 2 w 3 w_2 w_3 w 2 w 3 z z z z z z x 1 , x 2 , … , x n x_1,~x_2,\ldots,~x_n x 1 , x 2 , … , x n w w w w w w w 1 w_1 w 1 w 2 , … , w n w_2, \ldots, w_n w 2 , … , w n
定理9.3-1. (Schwarz-Christoffel變換) P \mathcal{P} P w 1 , w 2 , … , w n w_1, w_2,\ldots,w_n w 1 , w 2 , … , w n α k \alpha_k α k 0 ≤ α k < 2 π 0\le \alpha_k< 2\pi 0 ≤ α k < 2 π w = f ( z ) w=f(z) w = f ( z ) Im ( z ) > 0 \text{Im}(z)>0 Im ( z ) > 0 R ′ \mathcal{R}' R ′ f ( z ) f(z) f ( z )
d w d z = A ( z − x 1 ) α 1 / π − 1 ( z − x 2 ) α 2 / π − 1 ⋯ ( z − x n ) α n / π − 1 , \frac{dw}{dz}
=A (z-x_1)^{\alpha_1/\pi-1}
(z-x_2)^{\alpha_2/\pi-1}
\cdots
(z-x_n)^{\alpha_n/\pi-1}, d z d w = A ( z − x 1 ) α 1 / π − 1 ( z − x 2 ) α 2 / π − 1 ⋯ ( z − x n ) α n / π − 1 , 以及函數本身表為
w = f ( z ) = A ∫ 0 z ∏ k = 1 n ( ζ − x k ) α k / π − 1 d ζ + B , w = f(z) = A \int_0^z \prod_{k=1}^n (\zeta - x_k)^{\alpha_k/\pi-1} d\zeta + B, w = f ( z ) = A ∫ 0 z k = 1 ∏ n ( ζ − x k ) α k / π − 1 d ζ + B , 其中 A A A B B B
此定理所用被積函數的分母包含型如 ( z − x k ) 1 − α k π (z-x_k)^{1-\frac{\alpha_k}{\pi}} ( z − x k ) 1 − π α k
∫ d z ( z 2 − 1 ) 1 2 = i sin − 1 z = log [ z + ( z 2 − 1 ) 1 2 ] − i π 2 . \displaystyle \int\frac{dz}{(z^2-1)^\frac12} = i \sin^{-1} z
= \log\left[z+(z^2-1)^\frac12 \right]-i\frac{\pi}{2}. ∫ ( z 2 − 1 ) 2 1 d z = i sin − 1 z = log [ z + ( z 2 − 1 ) 2 1 ] − i 2 π . ∫ d z z 2 + 1 = tan − 1 z = i 1 2 log i + z i − z . \displaystyle \int\frac{dz}{z^2+1} = \tan^{-1} z
=i\frac12\log\frac{i+z}{i-z}. ∫ z 2 + 1 d z = tan − 1 z = i 2 1 log i − z i + z . ∫ d z z ( z 2 − 1 ) 1 2 = − sin − 1 1 z = i log [ 1 z + ( 1 z 2 − 1 ) 1 2 ] . \displaystyle \int\frac{dz}{z(z^2-1)^\frac12} =- \sin^{-1} \frac{1}{z}
=i \log\left[\frac1{z}+\left(\frac{1}{z^2}-1\right)^\frac12\right]. ∫ z ( z 2 − 1 ) 2 1 d z = − sin − 1 z 1 = i log [ z 1 + ( z 2 1 − 1 ) 2 1 ] . ∫ d z z ( z + 1 ) 1 2 = − 2 tanh − 1 ( z + 1 ) 1 2 = log 1 − ( z + 1 ) 1 2 1 + ( z + 1 ) 1 2 \displaystyle \int\frac{dz}{z(z+1)^\frac12} =- 2\tanh^{-1} (z+1)^\frac12
= \log\frac{1-(z+1)^\frac12}{1+(z+1)^\frac12} ∫ z ( z + 1 ) 2 1 d z = − 2 tanh − 1 ( z + 1 ) 2 1 = log 1 + ( z + 1 ) 2 1 1 − ( z + 1 ) 2 1 ∫ ( 1 − z 2 ) 1 2 d z = 1 2 [ z ( 1 − z 2 ) 1 2 + sin − 1 z ] = i 1 2 { z ( z 2 − 1 ) 1 2 + log [ z + ( z 2 − 1 ) 1 2 ] } . \displaystyle \int(1-z^2)^\frac12 dz
=\frac12\left[z(1-z^2)^\frac12+\sin^{-1}z\right]
=i\frac12 \left\{ z(z^2-1)^\frac12+\log\left[z+(z^2-1)^\frac12\right]\right\}. ∫ ( 1 − z 2 ) 2 1 d z = 2 1 [ z ( 1 − z 2 ) 2 1 + sin − 1 z ] = i 2 1 { z ( z 2 − 1 ) 2 1 + log [ z + ( z 2 − 1 ) 2 1 ] } .
Schwarz-Christoffel變換的基本思想是將複雜的幾何形狀通過變換轉化為簡單的形狀(如上半平面或圓盤),從而將複雜的邊界條件轉化為簡單的邊界條件,以便於求解。例如,在流體力學中,我們可能需要求解一個在某個複雜形狀的管道中流動的流體的速度場。這種問題通常很難直接求解。但是,如果我們可以找到一個Schwarz-Christoffel變換,將這個管道映射到一個矩形管道,那麼問題就變得簡單多了,因為矩形管道中的流動問題我們是知道如何求解的。儘管這個Schwarz-Christoffel變換在理論上可以將上半平面映射到任何多邊形,但在實際應用中,它最常用於映射到矩形或其他具有直邊的多邊形。
在實際應用中,Schwarz-Christoffel變換的求解通常需要通過數值方法來進行。首先,我們需要找到一個適當的變換,將複雜的幾何形狀轉換為簡單的形狀。這個變換的形式通常是由問題的幾何形狀決定的。然後,我們需要計算出變換的參數,這通常需要解決一個非線性的最優化問題。在求解了這個問題之後,我們就可以得到最終的變換,並將它應用到實際的問題中。
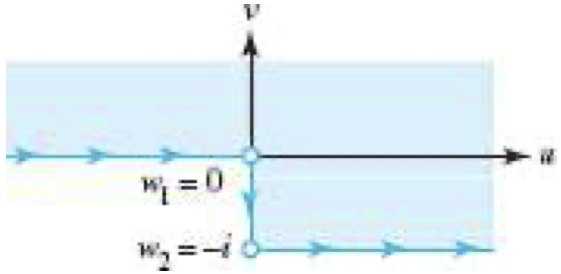
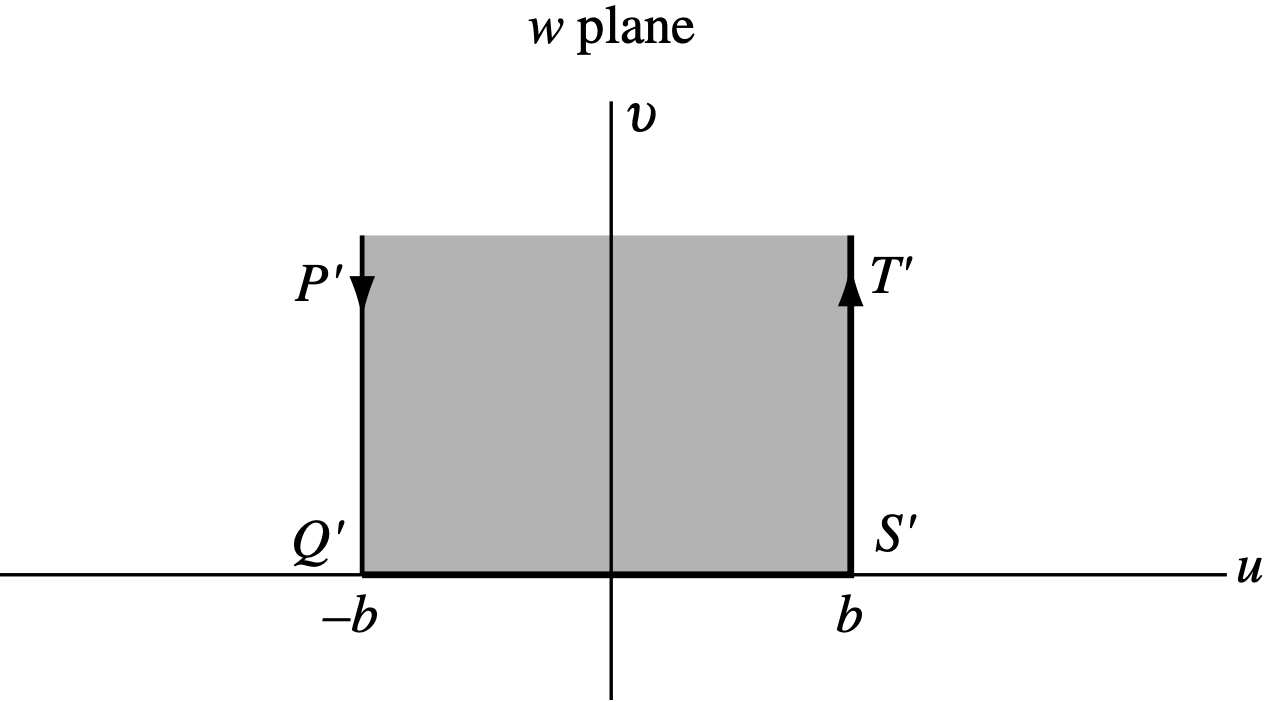
範例9.3-1. 計 算將上半平面映射到半無窮的長條型 ∣ Re w ∣ < b , Im w > 0 |\text{Re}~w|<b,~\text{Im}~w>0 ∣ Re w ∣ < b , Im w > 0
[解] 從圖形來看
d w d z = A ( z + 1 ) π / 2 π − 1 ( z − 1 ) π / 2 π − 1 \frac{d w}{d z}=A (z+1)^{\frac{\pi/2}{\pi}-1}
(z-1)^{\frac{\pi/2}{\pi}-1} d z d w = A ( z + 1 ) π π /2 − 1 ( z − 1 ) π π /2 − 1 積分可得
w = f ( z ) = A ∫ 0 z ( ζ + 1 ) − 1 2 ( ζ − 1 ) − 1 2 d z + B = A i ∫ 0 z 1 1 − ζ 2 d ζ + B = A i sin − 1 z + B . \begin{align*}
w=f(z)
&=A\int_0^z (\zeta+1)^{-\frac12}(\zeta-1)^{-\frac12} dz+B \\
&=\frac{A}{i}\int_0^z \frac{1}{\sqrt{1-\zeta^2}}d\zeta+B \\
&=\frac{A}{i}\sin^{-1} z+B.
\end{align*} w = f ( z ) = A ∫ 0 z ( ζ + 1 ) − 2 1 ( ζ − 1 ) − 2 1 d z + B = i A ∫ 0 z 1 − ζ 2 1 d ζ + B = i A sin − 1 z + B . 代入關係 f ( − 1 ) = − b f(-1)=-b f ( − 1 ) = − b f ( 1 ) = b f(1)=b f ( 1 ) = b
− i A sin − 1 ( − 1 ) + B = − b , − i A sin − 1 ( 1 ) + B = b , -iA\sin^{-1}(-1)+B=-b,\\
-iA\sin^{-1}(1)+B=b, − i A sin − 1 ( − 1 ) + B = − b , − i A sin − 1 ( 1 ) + B = b , 如此可得 B = 0 B=0 B = 0 A = i 2 b π A=i\frac{2b}{\pi} A = i π 2 b
w = f ( z ) = 2 b π sin − 1 z . w=f(z)=\frac{2b}{\pi}\sin^{-1}z. w = f ( z ) = π 2 b sin − 1 z . 又若 b = π / 2 b=\pi/2 b = π /2 w = f ( z ) = sin − 1 z w=f(z)=\sin^{-1}z w = f ( z ) = sin − 1 z
範例9.3-2. 驗證變換
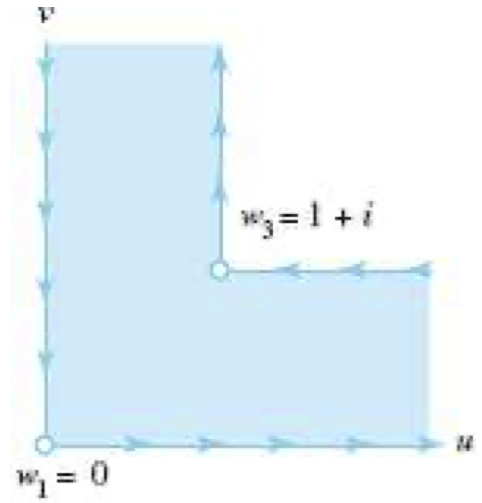
w = f ( z ) = 1 π sin − 1 z + i π sin − 1 1 z + 1 + i 2 , w=f(z)=\frac{1}{\pi} \sin^{-1} z+\frac{i}{\pi} \sin^{-1}\frac1z+\frac{1+i}{2}, w = f ( z ) = π 1 sin − 1 z + π i sin − 1 z 1 + 2 1 + i , 算將上半平面 Im z > 0 \text{Im}z >0 Im z > 0 { ( u , v ) : u ≥ 1 , v = 1 & u = 1 , v ≥ 1 } \{(u,v): u\ge 1, v=1~ \& ~u=1,v\ge1\} {( u , v ) : u ≥ 1 , v = 1 & u = 1 , v ≥ 1 }
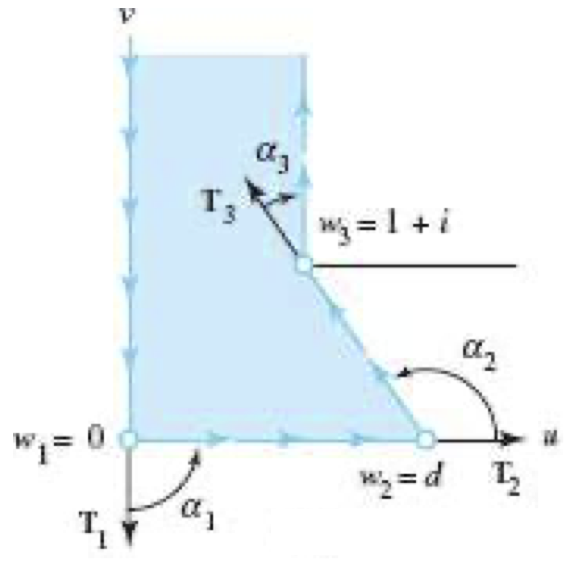
[解] 選擇 x 1 = − 1 , x 2 = 0 , x 3 = 1 , w 1 = 0 , w 2 = d , w 3 = 1 + i x_1=-1,~x_2=0,~x_3=1,~ w_1=0,~w_2=d,~w_3=1+i x 1 = − 1 , x 2 = 0 , x 3 = 1 , w 1 = 0 , w 2 = d , w 3 = 1 + i
則對應的 Schwarz-Christoffel 變換 g g g
g ′ ( z ) = A 1 ( z + 1 ) α 1 π − 1 ( z ) α 2 π − 1 ( z − 1 ) α 3 π − 1 g'(z)=A_1 (z+1)^{\frac{\alpha_1}{\pi}-1} (z)^{\frac{\alpha_2}{\pi}-1} (z-1)^{\frac{\alpha_3}{\pi}-1} g ′ ( z ) = A 1 ( z + 1 ) π α 1 − 1 ( z ) π α 2 − 1 ( z − 1 ) π α 3 − 1 其中 α 1 = π / 2 \alpha_1=\pi/2 α 1 = π /2 d → ∞ d\to \infty d → ∞ α 2 = 0 , α 3 = 3 π 2 \alpha_2=0,~\alpha_3=\frac{3\pi}{2} α 2 = 0 , α 3 = 2 3 π g → f g\to f g → f
f ′ ( z ) = A 1 ( z + 1 ) − 1 2 ( z ) − 1 ( z − 1 ) 1 2 = A 1 1 z ( z − 1 z + 1 ) 1 2 = A z − 1 z ( 1 − z 2 ) 1 2 , A = − i A 1 . f'(z)=A_1 (z+1)^{-\frac12} (z)^{-1} (z-1)^{\frac12}
=A_1\frac1{z}\left(\frac{z-1}{z+1}\right)^\frac12
=A\frac{z-1}{z(1-z^2)^\frac12},~A=-iA_1. f ′ ( z ) = A 1 ( z + 1 ) − 2 1 ( z ) − 1 ( z − 1 ) 2 1 = A 1 z 1 ( z + 1 z − 1 ) 2 1 = A z ( 1 − z 2 ) 2 1 z − 1 , A = − i A 1 . 積分可得
f ( z ) = A [ ∫ d z ( 1 − z 2 ) 1 2 − i d z z ( z 2 − 1 ) 1 2 ] = A [ sin − 1 z + i sin − 1 1 z ] + B . \begin{align*}
f(z) &= A\left[\int\frac{dz}{(1-z^2)^\frac12}-i\frac{dz}{z(z^2-1)\frac12}\right]\\
&=A \left[\sin^{-1}z+i\sin^{-1}\frac1z\right]+B.
\end{align*} f ( z ) = A [ ∫ ( 1 − z 2 ) 2 1 d z − i z ( z 2 − 1 ) 2 1 d z ] = A [ sin − 1 z + i sin − 1 z 1 ] + B . 由映射條件 f ( − 1 ) = 0 , f ( 1 ) = 1 + i f(-1)=0,~f(1)=1+i f ( − 1 ) = 0 , f ( 1 ) = 1 + i A = 1 / π , B = ( 1 + i ) / 2 A=1/\pi,~B=(1+i)/2 A = 1/ π , B = ( 1 + i ) /2
w = f ( z ) = 1 π sin − 1 z + i π sin − 1 1 z + 1 + i 2 . w=f(z)=\frac{1}{\pi}\sin^{-1}z+\frac{i}{\pi}\sin^{-1}\frac1z+\frac{1+i}{2}. w = f ( z ) = π 1 sin − 1 z + π i sin − 1 z 1 + 2 1 + i . 為所求。
範例9.3-2. 驗證變換 w = f ( z ) = 1 π ( z 2 − 1 ) 1 2 + 1 π Log [ z + ( z 2 − 1 ) 1 2 ] − i w=f(z)=\frac{1}{\pi}(z^2-1)^\frac12+\frac1{\pi}\text{Log}\left[z+(z^2-1)^\frac12\right]-i w = f ( z ) = π 1 ( z 2 − 1 ) 2 1 + π 1 Log [ z + ( z 2 − 1 ) 2 1 ] − i x 1 = − 1 , x 2 = 1 x_1=-1,~x_2=1 x 1 = − 1 , x 2 = 1
[解] 由於內部角為 α 1 = 3 π 2 , α 2 = π 2 \alpha_1=\frac{3\pi}{2},~\alpha_2=\frac{\pi}{2} α 1 = 2 3 π , α 2 = 2 π
f ′ ( z ) = A 1 ( z + 1 ) 1 2 ( z − 1 ) − 1 2 = A z + 1 ( z 2 − 1 ) 1 2 , A = − i A 1 , f'(z)=A_1(z+1)^\frac12(z-1)^{-\frac12}=A\frac{z+1}{(z^2-1)^\frac12},~A=-iA_1, f ′ ( z ) = A 1 ( z + 1 ) 2 1 ( z − 1 ) − 2 1 = A ( z 2 − 1 ) 2 1 z + 1 , A = − i A 1 , 積分可得
w = f ( z ) = A [ ∫ z ( z 2 − 1 ) 1 2 d z + ∫ 1 ( z 2 − 1 ) 1 2 d z ] = A [ ( z 2 − 1 ) 1 2 + Log [ z + ( z 2 − 1 ) 1 2 ] − i π 2 ] + B . \begin{align*}
w=f(z)&=A\left[\int \frac{z}{(z^2-1)^\frac12}dz+\int \frac{1}{(z^2-1)^\frac12}dz\right]\\
&=A\left[(z^2-1)^{\frac12}+\text{Log}\left[z+(z^2-1)^\frac12\right]-i\frac{\pi}{2}\right]+B.
\end{align*} w = f ( z ) = A [ ∫ ( z 2 − 1 ) 2 1 z d z + ∫ ( z 2 − 1 ) 2 1 1 d z ] = A [ ( z 2 − 1 ) 2 1 + Log [ z + ( z 2 − 1 ) 2 1 ] − i 2 π ] + B . 代入變換條件 f ( − 1 ) = 0 , f ( 1 ) = − i f(-1)=0,~f(1)=-i f ( − 1 ) = 0 , f ( 1 ) = − i
A Log ( − 1 ) − i π 2 A + B = 0 , − i π 2 A + B = − i , A~\text{Log}(-1)-i\frac{\pi}{2}A+B=0,\\
-i\frac{\pi}{2}A+B=-i, A Log ( − 1 ) − i 2 π A + B = 0 , − i 2 π A + B = − i , 得 A = 1 π , B = − i / 2 A=\frac1{\pi},~B=-i/2 A = π 1 , B = − i /2
w = f ( z ) = 1 π ( z 2 − 1 ) 1 2 + 1 π Log [ z + ( z 2 − 1 ) 1 2 ] − i . w=f(z)
=\frac1{\pi}(z^2-1)^{\frac12}+\frac{1}{\pi}\text{Log}\left[z+(z^2-1)^\frac12\right]-i. w = f ( z ) = π 1 ( z 2 − 1 ) 2 1 + π 1 Log [ z + ( z 2 − 1 ) 2 1 ] − i .
特殊變換 參考 [Zill-Shanahan]
1. 基本變換 2.對應到上半平面 3. 對應到圓形區域 4. 其他變換
習題 請驗證變換 w = f ( z ) = A ∫ 0 z ( ζ 2 − 1 ) − 3 / 4 d ζ + B w=f(z)=\displaystyle A \int_0^z (\zeta^2-1)^{-3/4}d\zeta+B w = f ( z ) = A ∫ 0 z ( ζ 2 − 1 ) − 3/4 d ζ + B A = 1 − i η , B = 1 + i 2 A=\frac{1-i}{\eta},~B=\frac{1+i}{2} A = η 1 − i , B = 2 1 + i η = A ∫ 0 − 1 ( ζ 2 − 1 ) − 3 / 4 d ζ ≈ 1.85 ( 1 + i ) \eta = \displaystyle A \int_0^{-1} (\zeta^2-1)^{-3/4}d\zeta\approx 1.85(1+i) η = A ∫ 0 − 1 ( ζ 2 − 1 ) − 3/4 d ζ ≈ 1.85 ( 1 + i ) w w w