本節目的在於利用留數定理計算微積分中的有理函數的瑕積分之值。一般而言瑕積分分成以下三類:
∫0∞f(x)dx=b→∞lim∫0bf(x)dx∫−∞0f(x)dx=a→−∞lim∫a0f(x)dx∫−∞∞f(x)dx=a→−∞lim∫acf(x)dx+b→∞lim∫cbf(x)dx, c∈R.(第一型)(第二型)(第三型) 因此只要上述極限值存在,則稱對應的瑕積分存在。若(第三型)的瑕積分存在,則其值亦可計算如下:
∫−∞∞f(x)dx=R→∞lim∫−RRf(x)dx. 範例8.3-1. 考慮瑕積分 ∫−∞∞x2+12xdx,由於 ∫x2+12xdx=ln(x2+1)+C, C∈R,得知
∫0∞x2+12xdx=b→∞lim∫0bx2+12xdx=b→∞limln(x2+1)0b=b→∞limln(b2+1)=∞, 亦即 ∫−∞∞x2+12xdx 不存在,然而
R→∞lim∫−RRx2+12xdx=R→∞limln(x2+1)−RR=0. 亦即 R→∞lim∫−RRf(x)dx 之值存在,不代表瑕積分 ∫−∞∞f(x)dx 存在。
有理函數積分
定義8.3-1. 設 f∈C(−∞,∞),則定義 Cauchy 主值 (principal value, P.V.)為
P.V.∫−∞∞f(x)dx=R→∞lim∫−RRf(x)dx. 範例8.3-2. P.V.∫−∞∞xdx=R→∞lim∫−RRxdx=R→∞lim2x2−RR=0 ,但 ∫−∞∞xdx 不存在,此因 b→∞lim∫0bxdx=∞。
範例8.3-3. 計算 P.V.∫−∞∞x2+11dx 之值。
[解]
P.V.∫−∞∞x2+11dx=R→∞lim∫−RRx2+11dx=R→∞limtan−1x−RR=R→∞lim2tan−1R=22π=π. 注意
∫−∞∞x2+11dx=a→−∞lim∫a0x2+11dx+b→∞lim∫0bx2+11dx=a→−∞limtan−1xa0+b→∞limtan−1x0b=−a→−∞limtan−1a+b→∞limtan−1b=−(−2π)+2−π=π. 因此 ∫−∞∞x2+11dx=P.V.∫−∞∞x2+11dx 。
定理8.3-1. 設 f(z)=Q(z)P(z),其中 deg(Q)≥deg(P)+2 。若 Q(x)=0, ∀x∈R ,則
P.V.∫−∞∞f(x)dx=2πij=1∑kRes[QP,zj], 其中 zj, j=1,2,…,k 為 f 落在上半平面之極點,即 Im(zj)≥0。
[證明]
參考下圖取積分路徑 C=CR∪([−R,R]×0),則
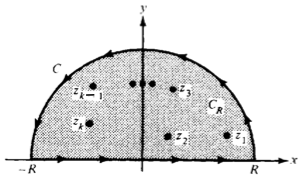
∫−RRf(x)dx=∮Cf(z)dz−∫CRf(z)dz=2πij=1∑kRRes[QP,zj]−∫CRQ(z)P(z)dz 其中 zj, 1≤j≤kR 為落在 Int(C) 內 QP 之極點。
Claim: R→∞lim∫CRf(z)dz=0。
設 n=deg(Q) 與 m=deg(P),則有 n≥m+2 以及可令
P(z)=amzm+am−1zm−1+⋯+a1z+a0,Q(z)=bnzm+bm−1zm−1+⋯+b1z+b0, 則
∣z∣→∞limQ(z)zP(z)=∣z∣→∞limznzm+1bn+bn−1z−1+⋯+b1z−n+1+b0z−nam+am−1z−1+⋯+a1z−m+1+a0z−m=0⋅bnam=0, 即
∀ε>0,∃Rε>0 s.t. ∣z∣≥Rε⟹Q(z)zP(z)<∣z∣πε. 取 R>Rε,則 ∀z∈CR⟹Q(z)zP(z)<∣z∣πε=πRε,因而
∫CRQ(z)P(z)dz≤∫CRQ(z)P(z)dz<∫CRπRεd∣z∣=ε, 即 R→∞lim∫CRf(z)dz=0。
因此由
R→∞lim∫−RRf(x)dx=R→∞lim∮Cf(z)dz−R→∞lim∫CRf(z)dz=R→∞lim∮Cf(z)dz 可知
P.V.∫−∞inftyf(x)dx=R→∞lim∫−RRf(x)dx=R→∞lim∮Cf(z)dz=R→∞lim2πij=1∑kRRes[QP,zj]=2πij=1∑kRes[QP,zj]. 其中 zj, 1≤j≤k 為落在上半平面內 QP 之極點。得證本定理。
範例8.3-4. 計算 ∫−∞∞ (1+x2)(4+x2)dx 之值。
[解]
由範例8.2-2知 ∫−∞∞1+x21dx 存在,且 ∫−∞∞4+x21dx 也隨之存在,又因
f(x)=(1+x2)(4+x2)1=31[1+x21−4+x21], 故 ∫−∞∞ (1+x2)(4+x2)dx 存在且其值等於 P.V.∫−∞∞ (1+x2)(4+x2)dx。
又因 (1+z2)(4+z2)=0⟹z=±i, ±2i,其中 z=i, 2i 落在上半平面,因此
Res[f,i]Res[f,2i]=z→ilim(z2+1)(z2+4)z−i=z→ilim(z+i)(z2+4)1=−6i,=z→2ilim(z2+1)(z2+4)z−2i=z→2ilim(z2+1)(z+2i)1=12i. 因此由定理8.3-1可得
P.V.∫−∞∞(1+x2)(4+x2)dx=2πi(−6i+12i)=6π. 此例積分也可計算如下:
∫−∞∞(1+x2)(4+x2)dx=31[∫−∞∞1+x2dx−21∫−∞∞1+(x/2)2d(x/2)]=31(π−21π)=6π.
範例8.3-5. 計算 ∫−∞∞(4+x2)4dx 之值。
[解]
由於當 ∣x∣>1 時,因 (4+x2)31<4+x21知 ∫−∞∞(4+x2)3dx≤∫−∞∞4+x2dx,因此 ∫−∞∞(4+x2)4dx 存在。
由於 z=2i 為 f(z)=(z4+4)31 落在上半平面的 3 階,因此
∫−∞∞4+x2dx=2πiRes[f,2i]=2πiz→2ilim2!1dz2d2(z2+4)3(z−3i)32i=2πiz→2ilim21dz2d2(z+2i)312i=2πiz→2ilim21dzd(z+2i)4−32i=2πiz→2ilim(z+2i)562i=2πi512i3=2563π.
定理8.3-1的作法,可以應用到更廣義的區域形式,如下例所示:
範例8.3-6. 計算 I=∫0∞1+x3dx 之值。
[解]
參考下圖之積分路徑,可知
I=∫0∞1+x3dx=R→∞lim∫C1z3+1dz. 由定理8.3-1之證明過程可得 R→∞lim∫CRz3+1dz=0。
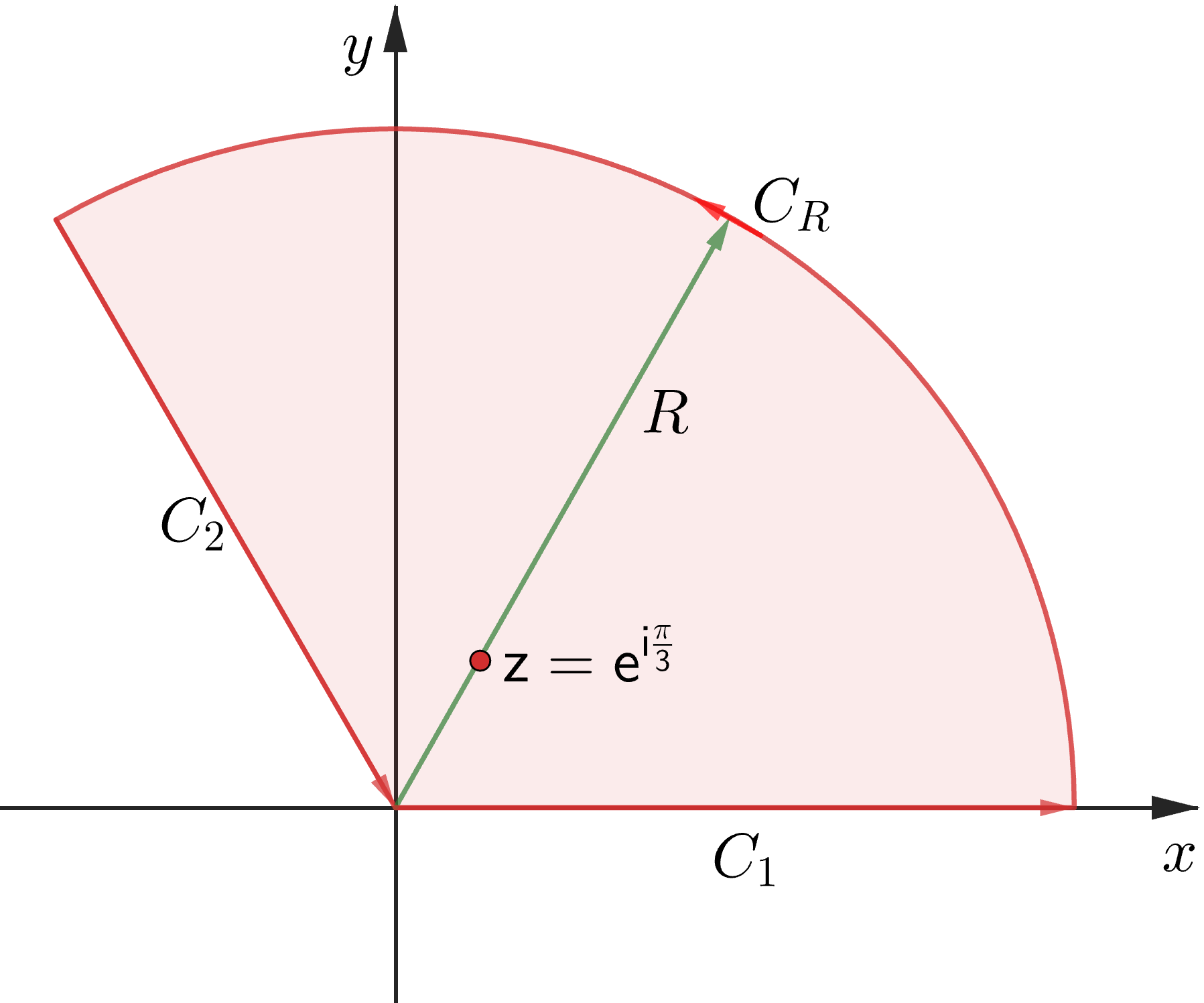
Claim: ∫C2z3+1dz=−ei32π∫C2z3+1dz。
令 C2={z=ρei32π∣ρ:R→0},若 z∈C2⟹dz=ei32πdρ,以及 z3=(ρei32π)3=ρ3 (這是為何 C2 延 θ=32π的原因)。
∫C2z3+1dz=∫R0ei32πρ3+1dρ=−ei32π∫0Rρ3+1dρ=−ei32π∫C1z3+1dz. 利用上述Claim可得
R→∞lim∫C1+CR+C2z3+1dz=(1−e−i32π)R→0lim∫C1z3+1dz=(1−e−i32π)I. 又在圍線 C=C1+CR+C2 之內有 z3+11 之單極點 z=ei3π,所以
R→∞lim∫Cz3+1dz=2πiRes[z3+11,ei3π]=2πiz→ei3πlimz3+1z−ei3π=2πiz→ei3πlim3z21=32πie−i32π 因此
I=1−ei32π1R→∞lim∮Cz3+1dz=32πi1−ei32πe−i32π=32πiei32π−ei34π1=332πi.
範例8.3-7. 令 I=P.V.∫−∞∞1+ebxeaxdx, 0<a<b ,證明
I=1−e2πiba1R→∞lim∫Γ1+Γ2+Γ3+Γ41+ebzeazdz 以及 I 之值,其中 Γ1, Γ2, Γ3 及 Γ4 如下圖所示。

[解]
令 C=Γ1+Γ2+Γ3+Γ4,又 I=R→∞lim∫−RR1+ebxeaxdx=R→∞lim∫Γ11+ebxeaxdx ,並立 f(z)=1+ebzeaz,則 f 之極點為 1+ebz=0 ,即 ebz=−1=ei(2k+1)π,得 z=bi(2k+1)π,其中 k∈Z,因此只有 z=biπ 被包含在積分路徑 C 之內。
Claim 1: R→∞lim∫Γ2,Γ41+ebzeazdz=0 。
設 z∈Γ2 則 z=R+it, t∈[0,b2π],因而-
∣eaz∣=eaR,∣1+ebz∣≥∣ebz∣−1=ebR−1, 由於
∫Γ21+ebzeazdz≤∫Γ21+ebzeazd∣z∣≤z∈Γ2max1+ebzeaz⋅L(Γ2)≤ebR−1eaRb2π, 所以
R→∞lim∫Γ21+ebzeazdz≤R→∞limebR−1eaRb2π=0. 設 z∈Γ4 則 z=−R+it, t∈[0,b2π],因而 ∣eaz∣≤eaR、 ∣ebz+1∣≥∣ebz∣−1=ebR−1,所以
∫Γ21+ebzeazdz≤∫Γ21+ebzeazd∣z∣≤z∈Γ2max1+ebzeaz⋅L(Γ2)≤ebR−1eaRb2π, 即
R→∞lim∫Γ21+ebzeazdz≤R→∞limebR−1eaRb2π=0. Claim 2: ∫Γ31+ebzeazdz=−eib2πa∫Γ11+ebzeazdz。
令 z∈Γ3,則 z=t+ib2π, t∈[−R,R] 且 dz=dt,因此
∫Γ31+ebzeazdz=∫R−R1+eb(t+ib2π)ea(t+ib2π)dz=∫R−R1+ebt+2πieateib2πadt=−eib2πa∫−RR1+ebtei2πeatdt=−eib2πa∫−RR1+ebteatdt=−eib2πa∫Γ11+ebzeazdz. 利用上述Claim 1與Claim 2可得
I=R→∞lim∫Γ11+ebzeazdz=1−eib2πa1R→∞lim∫Γ1+Γ2+Γ3+Γ41+ebzeazdz. 透過代數運算,可得
I=1−eib2πa1R→∞lim∫C1+ebzeazdz=1−eib2πa2πiRes[1+ebzeaz,ibπ]=1−eib2πa2πiz→ibπlim1+ebz(z−ibπ)eaz=1−eib2πa2πiz→ibπlimbebzeaz+a(z−ibπ)eaz=1−eib2πa2πibeiπeaibπ=−bπe−ibaπ−eibaπ2i=bπeibaπ−e−ibaπ2i=bsinbaππ.
如若 0<a<1,則由範例8.3-7知 P.V.∫−∞∞1+exeaxdx=sin(aπ)π。試問若欲計算 P.V.∫−∞∞ex−1eaxdx ,則圍線積分要如何取才行?
應用在級數求和
設 p(x) 為二階(含)以上實係數多項式且無整數零點,即 p(k)=0, ∀k∈Z。欲計算 k=0∑∞p(k)1 或 k=0∑∞p(k)(−1)k 之值,則可以從 cotπz 或 cscπz 之極點來著手,亦即可考慮函數 F(z)=p(z)πcotπz的函數,則此函數之極點除了 p(z) 的零點外,尚有 cotπz 之極點,即 sinπz=0,可得 πz=kπ,即 z=k=0,±1,±2,…。
以下先考慮一般形的級數和 n=0∑∞f(n),取以下的圍線 CN :
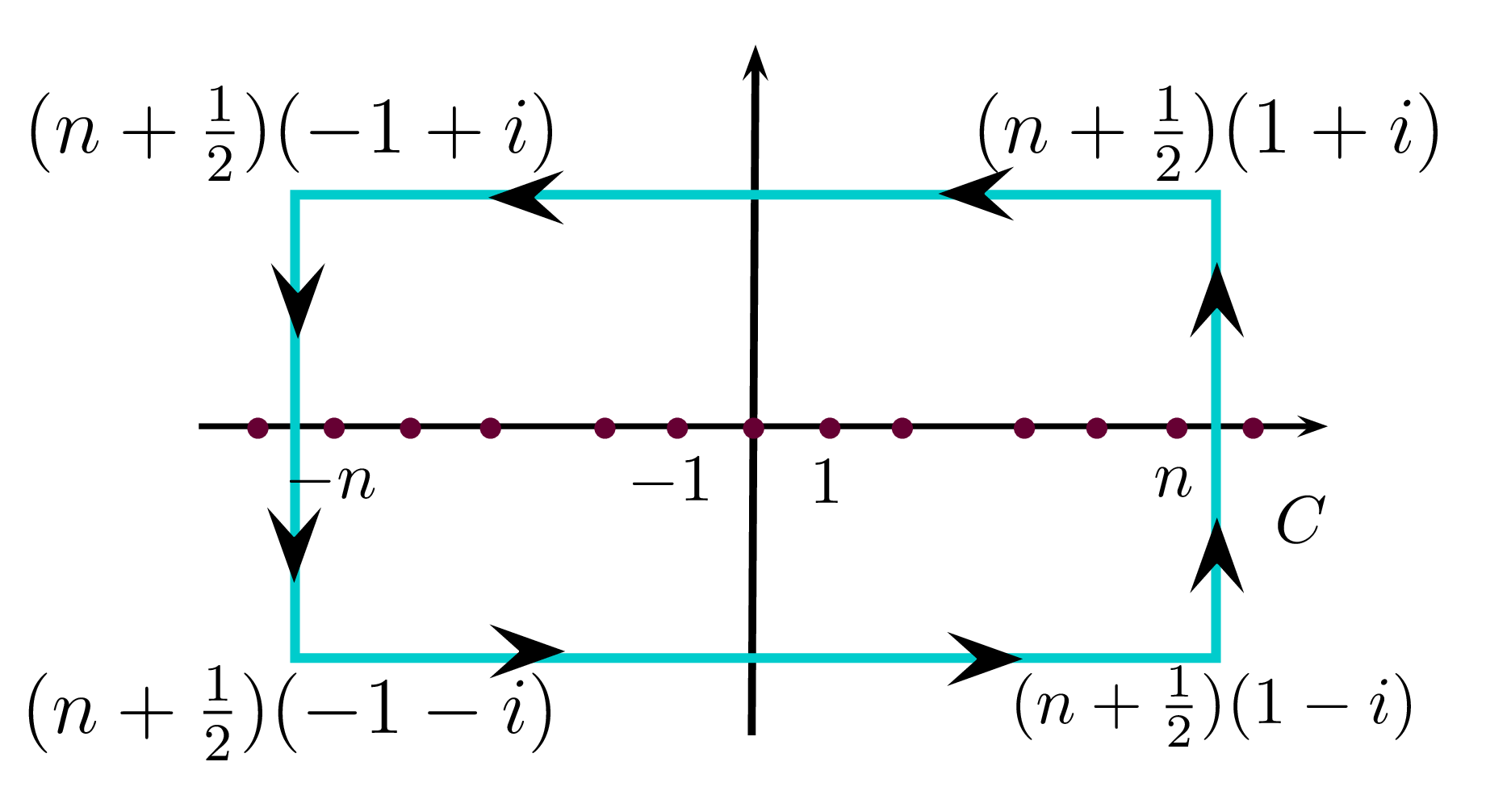 圖8.3.1 圍線 CN 圖形,其四個邊從底邊順時間數,分別為路徑 Γ1, Γ2, Γ3, Γ4。
圖8.3.1 圍線 CN 圖形,其四個邊從底邊順時間數,分別為路徑 Γ1, Γ2, Γ3, Γ4。即
CN=Γ1+Γ2+Γ3+Γ4, 其中
Γ1:z=(N+21)(t−i), t∈[−1,1],Γ3:z=(N+21)(−t+i), t∈[−1,1],Γ2:z=(N+21)(1+ti), t∈[−1,1],Γ4:z=(N+21)(−1−ti), t∈[−1,1]. 針對此圍線,函數 F 之積分為
∮CNF(z)dz=2πik=−N∑NRes[F,k]+2πij=1∑rNRes[F,zpj] 其中 zpj 為 F(z) 在圍線 CN 內之第 j 個零點,總數為 rN。
引理8.3-1. CN 如圖8.3.1所示,則於此圍線上 ∣cot(πz)∣<A 其中 A 為常數。
[證明]
(參考[SOCV]) 設 z=x+iy∈CN 時,分成 y<−21、 −21≤y≤21 與 y>21 等情形。
Case 1: y>21。 此情形下
∣cotπz)∣=∣eiπz−e−iπz∣∣eiπz+e−iπz∣=∣eiπx−πy−e−iπx+πy∣∣eiπx−πy+e−iπx+πy∣≤∣e−iπx+πy∣−∣eiπx−πy∣∣eiπx−πy∣+∣e−iπx+πy∣=eπy−e−πye−πy+eπy=1−e−2πy1+e−2πy≤1−e−π1+e−π=coth2π=A1 Case 2: y<−21。 此情形下
∣cotπz)∣≤∣e−iπx+πy∣−∣eiπx−πy∣∣eiπx−πy∣+∣e−iπx+πy∣=e−πy−eπye−πy+eπy=1−e2πy1+e2πy≤1−e−π1+e−π=coth2π=A1 Case 3: −21≤y≤21。 當 z∈Γ2,即 z=N+21+iy ,則
∣cotπz)∣=∣cotπ(N+21+iy)∣=∣cot(2π+iπy)∣=∣tanhπy∣≤tanh2π=A2, 而當 z∈Γ4,即 z=−(N+21)+iy ,則
∣cotπz)∣=∣cotπ(−N−21+iy)∣=∣cot(−2π+iπy)∣=∣tanhπy∣≤tanh2π=A2, 因此選擇 A=max{A1,A2}=A1 與 N 無關。
定理8.3-2. 設 f(z) 延如圖8.3.1的 CN 路徑滿足 ∣f(z)∣≤M/∣z∣m, m>1, M 為與 N 無關之常數,則
n=−∞∑∞f(n)=−j=1∑kRes[f(z)πcot(πz),zpj], 其中 zpj 為 f(z) 在複數平面的第 j 個極點,j=1,2,…,k。
[證明]
(參考[SOCV]) 設 f(z) 的極點是有限多個來討論;一旦其極點是無限多個時,先考量落在 CN 內,再透過 N→∞ 的極限來證明即可。
選定 N 如圖8.3.1包含所有 f(z) 之極點,而 cotπz 對應的單極點為 z=0, ±1, ±2,…。
πcotπzf(z) 在單極點 z=0, ±1, ±2,…。的留數為
z→nlim(z−n)πcot(πz)f(z)=z→nlimπsinπz(z−n)cosπzf(z)(=00)=z→nlimππcosπzcos(πz)f(z)+(z−n)[−πsin(πz)f(z)+cos(πz)f′(z)]=f(n). 注意: f(z) 在 z=n 不會有極點,否則無窮級數和n=−∞∑∞f(n) 不存在。因此
∮CNπcot(πz)f(z)dz=n=−N∑Nf(n)+SN 其中 SN 為在 CN 內 πcot(πz)f(z) 在 f(z) 的極點之留數,即 SN=2πij=1∑kNRes[f,zpj],其中 kN 為在 CN 內 f(z) 之極點總數。
由引理8.3-1可得
∮CNπcot(πz)f(z)dz≤πz∈CNmax∣cot(πz)∮CN∣z∣mMdz≤NmπAM∮CNd∣z∣=NmπAM(8N+4). 因此
N→∞lim∮CNπcot(πz)f(z)dz=0⟹N→∞lim∮CNπcot(πz)f(z)dz=0. 如此可得
N→∞lim∮CNπcot(πz)f(z)dz=0=n=−∞∑∞f(n)+S,N→∞limSN=S. 得證。
範例8.3-8. 證明 n=−∞∑∞n2+a21=aπcothπa 其中 a>0。
[解]
令 f(z)=z2+a21 ,極點為 z=±ai,有關的留數為
Res[πcot(πz)f(z),ai]=z→ailim(z−ai)(z+ai)(z−ai)πcot(πz)=2aiπcot(πai)=−2aπcoth(πa) 同理可得, Res[πcot(πz)f(z),−ai]=−2aπcoth(πa)。此函數滿足 ∣f(z)∣≤∣z∣21,因此由定理8.3-2 得
n=−∞∑∞f(n)=−Res[πcot(πz)f(z),ai]−Res[πcot(πz)f(z),−ai]=aπcoth(πa).
推論8.3-1. 設 f(z)=Q(z)P(z),其中 P(z) 與 Q(z) 為多項式滿足 deg(Q)≥deg(P)+2 的條件,且 f(z) 之極點為 zp1, zp2, …,zpk,並沒有落在整數上的極點,則
n=−∞∑∞Q(n)P(n)=−j=1∑kRes[Q(z)πcot(πz)P(z),zpj]. 推論8.3-1 之特例如下:
推論8.3-2. 設 f(z)=p(z)1,其中 p(z) 大於或等於二階多項式條件,且 p(z) 之零點為 zp1, zp2, …,zpk,並且沒有落在整數點上,則
n=−∞∑∞p(n)1=−j=1∑kRes[p(z)πcot(πz),zpj].
範例8.3.3. 證明 n=1∑∞n21=6π
[解]
計算在 z=k 與 z=0 (三階極點)之留數:
k=0∈Zz→klim(z−k)z2πcot(πz)=k=0∈Zz→klimz2sin(πz)(z−k)πcos(πz)=k=0∈Zz→klim2zsin(πz)+z2πcos(πz)πcos(πz)−(z−k)π2sin(πz)(=00)=k2πcos(kπ)πcos(kz)=k21 與
z→0lim2!1dz2d2(z2z3πcot(πz))=z→0lim2!1dz2d2(zπcot(πz))=z→0lim21dzd(πcot(πz)+zπ2csc2(πz))=z→0lim21(−2π2csc2(πz)+2zπ3csc2(πz)cot(πz))=π2z→0lim(−csc2(πz)+zπcsc2(πz)cot(πz))=π2z→0lim(sin3(πz)zπcos(πz)−sin2(πz)1)=π2z→0limsin3(πz)zπcos(πz)−sin(πz)(=00)=π2z→0lim3sin2(πz)cos(πz)πcos(πz)−zπ2sin(πz)−πcos(πz)=π2z→0lim3sin(πz)cos(πz)−zπ(=00)=π2z→0lim3πcos2(πz)−3πsin2(πz)−π=π2⋅3π−π=−3π2. 因此由推論8.3-2得
k=1∑∞k21=21(k=−∞∑−1k21+k=1∑∞k21)=−21Res[z2πcotπz,0]=6π2.
沿用上面的討論,留數定理可以應用在下面類型的無窮級數計算,歸納如下:
| 級數 | 方法 |
| n=−∞∑∞f(n) | 使用 ∮CNf(z)πcot(πz)dz ,其中 CN 是以 (n+21)(±1±i) 為頂點正方形 |
| n=−∞∑∞(−1)nf(n) | 使用 ∮CNf(z)πcsc(πz)dz ,其中 CN 是以 (n+21)(±1±i) 為頂點正方形 |
| n=−∞∑∞f(n+21) | 使用 ∮CNf(z)πtan(πz)dz ,其中 CN 是以 n(±1±i) 為頂點正方形 |
| n=−∞∑∞(−1)nf(n+21) | 使用 ∮CNf(z)πsec(πz)dz ,其中 CN 是以 n(±1±i) 為頂點正方形 |
習題
- 證明 n=1∑∞n2+a21=2aπcothaπ−2a21 其中 a>0。
- 證明 n=1∑∞n41=90π4。
- 證明 n=−∞∑∞n2(−1)n=−12π2。
- 證明 n=1∑∞n4(−1)n=7207π4。
- 證明 n=1∑∞(a+n)2(−1)n=π2cot(πa)csc(πa)。
參考文獻
[SOCV] Spiegel, M. R., Lipschutz, S., Schiller, J. .J., Spellman, D., Schaum’s Outline of Complex Variables, 2nd ed., McGraw-Hill, Inc, USA, 2009.



