Laurent 定理
本節假設 f(z) 除 z=0 外均為解析。
範例7.3-1. 設 f(z)=z31 與 g(z)=ez=n=0∑∞n!zn,以及 h(z)=f(z)⋅g(z),則當 z=0時, h(z) 有下列的級數表示法:
h(z)=z31n=0∑∞n!zn=z31+z21+2!z1+3!1+4!z+⋯=n=−3∑∞(n+3)!zn 此例可知函數可以展開成級數的區域,我們能否將該級數的定義域從原本的圓盤(鄰域)之內改變成在環(annulus)之內?
定義7.3-1. (Laurent 級數) 設 cn∈C, n=±1,±2,…,在 z=α 的 Laurent 級數的一般形式為:
f(z)=n=−∞∑∞cn(z−α)n=n=1∑∞c−n(z−α)−n+n=0∑∞cn(z−α)n≜fs(z)+fa(z) 其中 fs(z)=n=1∑∞c−n(z−α)−n 稱為 f 的奇異分項(singular or principal part), fa(z)=n=0∑∞cn(z−α)n 稱為 f 的解析分項(analytic or regular part)。
定義7.3-2. (環, annulus) 給定 0≤r<R, 以 α 為中心、半徑為 r 與 R 之環 A(α,r,R) 定義為 A(α,r,R)={z∈C : r<∣z−α∣<R},而閉環則定義為 A(α,r,R)={z∈C : r≤∣z−α∣≤R} 。

從環的定義,可知環和圓盤的關係有 DR∗(α)=A(α,0,R) , DR∗(α)=A(α,0,R) , A(α,r,R)=DR(α)−Dr(α),以及 A(α,r,R)=DR(α)−Dr(α)。
由於 Laurent 級數的解析分項之型式和 Taylor 級數相同,當 c−n=0, n≥1 時,則 Laurent 級數等於 Taylor 級數,因此 Laurent 級數明顯地為 Taylor 級數的延伸。此外 Laurent 級數 f(z) 在 z=α 為非解析,但會存在一個環,使 f(z) 在環上為解析。
定理7.3-1. 設 Laurent 級數n=−∞∑+∞cn(z−α)n 在環 A(α,r,R)上收斂,則此級數在閉環 A(α,s,t) 為均勻收斂,其中 r<s<t<R。
註: R=n→∞lim∣cncn+1∣1=n→∞limsup∣cn∣1/n1 以及 r1=n→∞limc−nc−(n+1)1=n→∞limsup∣c−n∣1/n1。
[證明]
(i) 由定義7.3-1知 n=0∑∞cn(z−α)n 在 Dt(α) 為均勻收斂。
(ii) Claim: n=1∑∞c−n(z−α)−n 在 E={z:∣z−α∣≥s}為均勻收斂。
∀z∈E, ∣z−α∣n1≤sn1,取 Mk=∣c−ksk1∣,由根號測試法知 n=0∑∞Mk 收斂,由於 ∣c−n(z−α)−n∣≤M, ∀n∈N,則由 Weierstrass M-檢測知所求成立。
由(i)(ii)得證本定理。
若 Laurent 級數在 z1 點收斂表示 fs(z1)=n=1∑∞c−n(z1−α)−n 及 fa(z1)=n=0∑∞cn(z1−α)n 在 z1 點同時收斂。
設
fa(z)=n=0∑∞cn(z−α)n 之收斂半徑為 Ra, 即
Ra1=n→∞limsup∣cn∣∣cn+1∣ 
因此級數 fa(z) 在 ∣z−z0∣≤ρ<Ra 內均勻收斂,而在 DRa(α) 內收斂。此外在 ∣z−α∣=Ra 上無法判定是否收斂,必須進一步計算;在 ∣z−α∣>Ra為發散。
至於 fs(z)=n=1∑∞c−n(z−α)−n 是否有收斂半徑存在?令 (z−α)−n=sn, c−n=bn, 則 fs(z) 可改寫為
fs(z)=n=1∑∞bnsn 為 s 之冪級數,設其收斂半徑為 Rs,即
Rs1=n→∞limsupbnbn+1=n→∞limsupc−nc−(n+1) 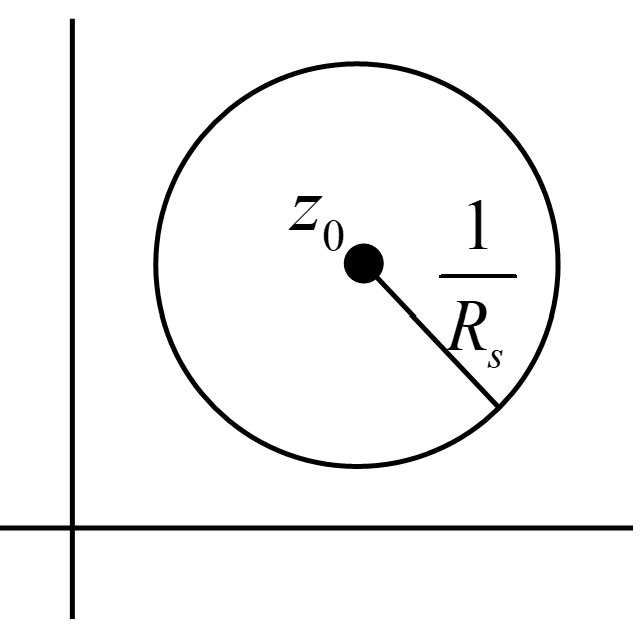
則 ∀∣s∣<Rs,fs(z)=n=1∑∞bnsn 為絕對收斂,即當 ∣z−α∣≥ρ>Rs1時, fs(z)=n=1∑∞c−n(z−α)−n 是均勻收斂的,而在 ∣z−α∣=Rs1 時則無法判定是否收斂,至於 ∣z−α∣<Rs1 則為發散。
歸納而言,對整個Laurent 級數來說
- 若 Rs1>Ra,則級數n=−∞∑∞cn(z1−α)n 到處發散。
- 若 Rs1=Ra,級數除了 ∣z−α∣=Ra 圓上的點以外都是發散。
- 若 Rs1<Ra,則級數 n=−∞∑∞cn(z1−α)n 在開環 Rs1<∣z−α∣<Ra 內收斂; 而在閉環 Rs1<rs≤∣z−α∣≤ρa<Ra 內均勻收斂;在 ∣z−α∣>Ra、 ∣z−α∣<Rs1 為發散;在 ∣z−α∣=Ra 與 ∣z−α∣=Rs1上無法判斷。
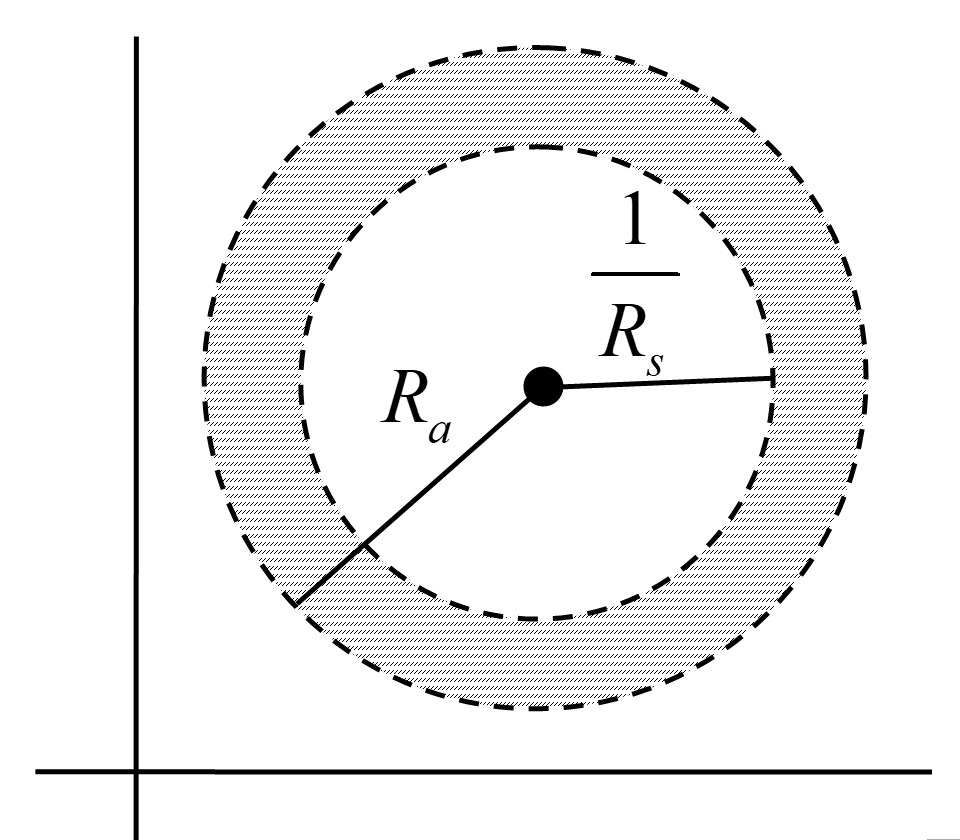
此外 fa 在 ∣z−z0∣<Ra 內解析,而 fs 在 ∣z−z0∣>Rs1 解析,得出 f(z)=fs(z)+fa(z)在 Rs1<∣z−z0∣<Ra 內解析。
定理7.3-2. (Laurent 定理) 設 0≤r<R 且函數 f 在圓環 r<∣z−α∣<R 內解析,則環內任一點 z0, f 有下列的 Laurent 級數表示法:
f(z0)=n=−∞∑∞cn(z0−α)n=n=1∑∞c−n(z0−α)−n+n=0∑∞cn(z0−α)n 其中
cn=2πi1∮Cρ+(α)(z−α)nf(z)dz,c−n=2πi1∮Cρ+(α)(z−α)−n+1f(z),r<ρ<R. 此外,此級數的在 A(α,s,t) 是均勻收斂的,其中 0≤r<s<t<R。
[證明]
在環 D 內取3個圓 C0:∣z−z0∣=r,C1:∣z−α∣=r1 及 C2:∣z−α∣=r2, r1<r2:
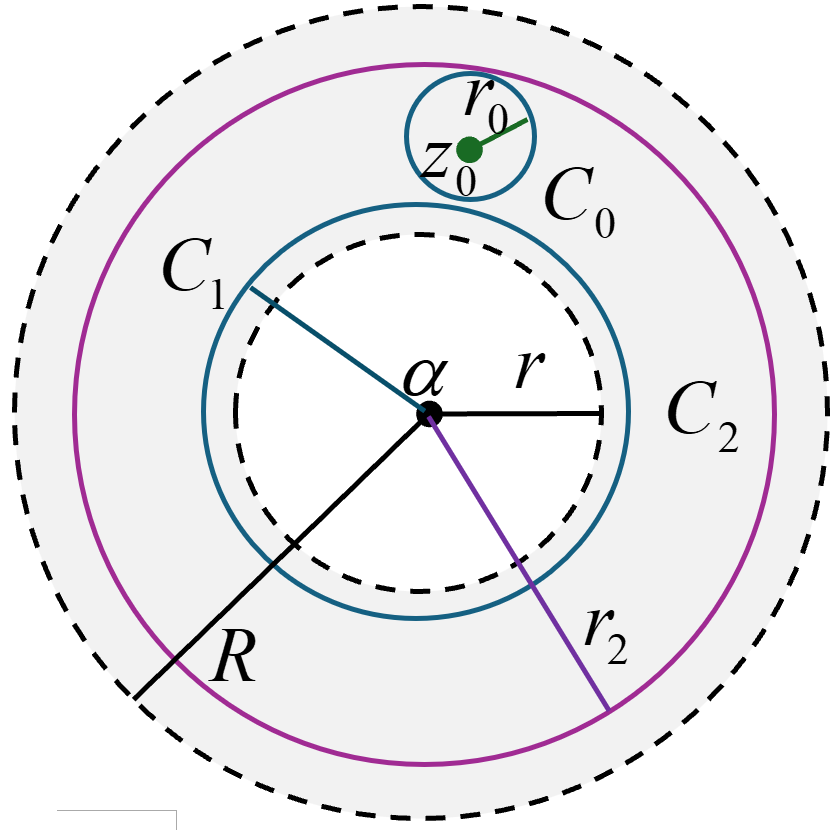
設 z0 為環內任意一點,且 r1<∣z0−α∣<r2 ,由於 z−z0f(z) 在 A(α,r1,r2)解析,則由Gauchy-Gousart變形定理得知
f(z0)=2πi1∮C0z−z0f(z)dz=2πi1∮C2z−z0f(z)dz−2πi1∮C1z−z0f(z)dz. 利用引理7.2-1公式可知:當 z∈C2 時
z−z01=(z−α)−(z0−α)1=z−α1(1−z−αz0−α1)=z−α1n=0∑∞(z−αz0−α)n=n=0∑∞(z−α)n+1(z0−α)n, u.c. 於z−αz0−α<1, 當 z∈C1 時
z−z01=(z0−α)−(z−α)−1=z0−α−1(1−z0−αz−α1)=z0−α−1n=0∑∞(z0−αz−α)n=−n=0∑∞(z0−α)n+1(z−α)n, u.c. on z0−αz−α<1. 所以
f(z0)=2πi1∮C2z−αf(z)dz−2πi1∮C1z−αf(z)dz=2πi1∮C2n=0∑∞(z−α)n+1f(z)dz(z0−α)n+2πi1∮C1n=0∑∞f(z)(z−α)ndz(z0−α)n+11=u.c.n=0∑∞[2πi1∮C2(z−α)n+1f(z)dz](z0−α)n+n=0∑∞[2πi1∮C1f(z)(z−α)ndz](z0−α)n+11=n=0∑∞[2πi1∮C1(z−α)−nf(z)dz](z0−α)n+11+n=0∑∞[2πi1∮C2(z−α)n+1f(z)dz](z0−α)n=n=1∑∞[2πi1∮C1(z−α)−n+1f(z)dz](z0−α)n1+n=0∑∞[2πi1∮C2(z−α)n+1f(z)dz](z0−α)n=n=1∑∞[2πi1∮Cρ+(α)(z−α)−n+1f(z)dz](z0−α)n1+n=0∑∞[2πi1∮Cρ+(α)(z−α)n+1f(z)dz](z0−α)n=n=1∑∞c−n(z−α)−n+n=0∑∞cn(z−α)n,∀z0∈A(α,r,R). 其中 0≤r<ρ<R。■
例題7.3-2. 已知 f(z)=1−z1 於 ∣z−0∣<1 以及 ∣z−0∣>1 為解析,求其對 z=0 之 Laurent 級數。
[解]
- 由於在 ∣z∣<1 解析,所以
f(z)=fa(z)=n=0∑∞cn(z−α)n,cn=2πi1∮Cρ+(α)(z−α)n+1f(z)dz. (a) 直接令 Cρ+(0)={z=ρeiθ:0≤θ≤2π},
∮Cρ+(0)zn+1f(z)dz=∫02π(1−ρeiθ)ρn+1ei(n+1)θρieiθdθ=i∫02π(1−ρeiθ)ρ−ne−inθdθ 由於 ∣ρeiθ∣<1,因此可以將 1−ρeiθ1進行幾何級數展開,即
∮Cρ+(0)zn+1f(z)dz=i∫02πρ−ne−inθk=0∑∞ρkeikθdθ=ik=0∑∞ρk−n∫02πei(k−n)θdθ 因
∫02πeinθdθ={2π,0,n=0,n=0. 可得
cn=2πi1∮Cρ+(0)(z−0)n+1f(z)=2π1k=0∑∞ρk−n∫02πei(k−n)θdθ(k=n 時有非零積分值)=2π12π=1. (b) 利用Cauchy積分公式
f(n)(α)=2πin!∮Cρ+(α)(z−α)n+1f(z)dz 因此 cn=n!1f(n)(α),加上直接計算得 f(n)(z)=(1−z)n+1n!,如此 f(n)(0)=n! 即 cn=1。
(c) 使用幾何級數 1−z1=1+z+z2+z3+⋯,即 cn=1。
整理可得:
f(z)=1−z1=1+z+z2+z3+⋯,∣z∣<1. - 由於在 ∣z∣>1 解析,所以
f(z)=fs(z)=n=1∑∞c−n(z−α)−n,c−n=2πi1∮Cρ+(α)(z−α)−n+1f(z)dz. 於此利用幾何級數來計算:
f(z)=1−z1=−z11−z11=−z1[1+z1+z21+z31+⋯]=−(z1+z21+z31+z41+⋯),∣z∣>1.
例題7.3-3. 求 f(z)=2+z−z23 在下列區域之 Laurent 級數:
(a) ∣z∣<1, (b) 1<∣z∣<2, (c) ∣z∣>2。
[解]
因 f(z)=2+z−z23=(z+1)(2−z)3=z+11+2−z1 且
1+z1=⎩⎨⎧1−(−z)1=1−z+z2−z3+−⋯=n=0∑∞(−1)nzn,z11−(−z1)1=z1−z21+z31−z41+−⋯=n=1∑∞(−1)n+1zn1,∣z∣<1,∣z∣>1. 以及
2−z1=⎩⎨⎧211−2z1=21[1+2z+4z2+8z3+⋯]=n=0∑∞2n+1zn,−z11−z21=−z1[1+z2+z24+z38+⋯]=n=1∑∞−zn2n−1,∣z∣<2,∣z∣>2. (b) 對 z∈D1(0) 而言,
f(z)=2+z−z23=n=1∑∞[(−1)n+2n+11]zn. (b) 對 z∈A(0,1,2) 而言,
f(z)=2+z−z23=n=1∑∞(−1)n+1z−n+n=0∑∞2n+1zn. (c) 對 {z : ∣z∣>2}r 而言,
f(z)=2+z−z23=n=1∑∞[(−1)n+1−2n−1]z−n.
唯一性與導函數
定理7.3-3. 設 f∈A(A(α,r,R)) 且函數 f(z)=n=−∞∑∞cn(z−α)n, ∀z∈A(α,r,R),下列敘述成立:
(1) 若 f(z) 亦可以表示成 f(z)=n=−∞∑∞bn(z−α)n, 則 bn=cn。
(2) f′(z)=n=−∞∑∞ncnzn−1, ∀z∈A(α,r,R)。
[證明]
設 r<ρ<R,由於
cn=2πi1∮Cρ+(α)(z−α)n+1f(z)dz=2πi1∮Cρ+(α)(z−α)−(n+1)m=−∞∑∞bm(z−α)m dz=m=−∞∑∞2πibm∮Cρ+(α)(z−α)m−n−1dz 由 Cρ+(α) 之參數式為 z=α+ρeiθ, θ∈[0,2π],可得
∮Cρ+(α)(z−α)m−n−1dz=∫02πρm−n−1ei(m−n−1)θρieiθdθ=iρm−n∫02πei(m−n)θdθ={2πi,0,m=n,m=n. 代入上式可得
cn=bn2πi2πi=bn. 又利用定理4.4-3. 可計算出 f′(z) 之公式。■
例題7.3-4. 計算 f(z)=z4cosz−1 以 α=0為展開中心之 Laurent 級數。
[解]
因 cosz−1=n=0∑∞(−1)n(2n)!z2n−1=n=1∑∞(−1)n(2n)!z2n,∀z∈C.
如此則有
f(z)=z4cosz−1=z41n=1∑∞(−1)n(2n)!z2n=n=1∑∞(−1)n(2n)!z2n−4=−2z21+241−720z2+−⋯, ∀∣z∣>1.
例題7.3-3 計算 f(z)=z4cosz−1 以 α=0為展開中心之 Laurent 級數。
[解]
因 cosz−1=n=0∑∞(−1)n(2n)!z2n−1=n=1∑∞(−1)n(2n)!z2n,∀z∈C-,如此則有
f(z)=z4cosz−1=z41n=1∑∞(−1)n(2n)!z2n=n=1∑∞(−1)n(2n)!z2n−4=−2z21+241−720z2+−⋯, ∀∣z∣>0.
例題7.3-4 計算 f(z)=e−z21 以 α=0為展開中心之 Laurent 級數。
[解]
因 ez=n=0∑∞n!zn,∀z∈C, 如此則有
f(z)=e−z21=n=0∑∞n!(−1)nz2n1=1−z21+2!1z41−3!1z61+−⋯, ∀∣z∣>0.




