三角函數
複數的三角函數定義如下:
定義5.4-1. 令 z∈C,
sin(z)=n=0∑∞(−1)n(2n+1)!z2n+1,cos(z)=n=0∑∞(−1)n(2n)!z2n,(5.4-1a) 以及
tan(z)=cos(z)sin(z), cot(z)=sin(z)cos(z), sec(z)=cos(z)1, csc(z)=sin(z)1.(5.4-1b)
實數時三角函數的 sin(x), cos(x)的絕對值小於等於1,但在複數系內是否仍然成立?
範例5.4-1. 請問 ∣sin(z)∣≤1, ∀z∈C 是否成立?
[解]
考慮當 z=1+i時,
(1+i)2n+1=(2i)n(1+i), 即
sin(1+i)=(1+i)−3!(1+i)3+5!(1+i)5−7!(1+i)7+−⋯=(1+i)[1−3!2i+5!−4−7!−8i+9!16+⋯]=[1−3!2i+5!−4−7!−8i+9!16+⋯]+i[1−3!2i+5!−4−7!−8i+9!16+⋯]=(1+3!2−5!4−7!8+9!16+−⋯)+i(1−3!2−5!4+7!8+9!16+−⋯),≈1.29846+0.63496i 因此 ∣sin(1+i)∣>1,可知敘述 ∣sin(z)∣≤1, ∀z∈C 不成立。
三角函數的性質說明如下:
性質
- 由定義5.3-1知
dzdsin(z)dzdcos(z)=n=0∑∞(−1)ndzd(2n+1)!z2n+1=n=0∑∞(−1)n(2n)!z2n=cos(z),=n=1∑∞(−1)ndzd(2n)!z2n=n=1∑∞(−1)n(2n−1)!z2n−1=n=0∑∞(−1)n+1(2n)!z2n=−sin(z).
- sin(−z)=n=0∑∞(−1)n(2n+1)!(−z)2n+1=n=0∑∞(−1)n(2n+1)!−z2n+1=−sin(z),
cos(−z)=n=0∑∞(−1)n(2n)!(−z)2n=n=0∑∞(−1)n(2n)!z2n=cos(z)。
- 由於 in={(−1)ki,(−1)k,n=2k+1,n=2k,,故
eiz=n=0∑∞n!(iz)n=n=0∑∞n!inzn=k=0∑∞(2k)!(i)2kz2k+k=0∑∞(2k+1)!(i)2k+1z2k+1=k=0∑∞(2k)!(−1)kz2k+ik=0∑∞(2k+1)!(−1)kz2k+1=cos(z)+isin(z), 以及 e−iz=cos(z)−isin(z),因此
cos(z)=2eiz+e−iz,sin(z)=2ieiz−e−iz.
- 驗證實數的關係 sin2(x)+cos2(x)=1, ∀x∈R,在複數是否仍然成立。
sin2(z)+cos2(z)=(2ieiz−e−iz)2+(2eiz+e−iz)2=41[−(e2iz−2+e−2iz)+(e2iz+2+e−2iz)]=1, ∀z∈C,即此恆等式仍然成立。
- 驗證實數的關係 sin(x1+x2)=sin(x1)cos(x2)+cos(x1)sin(x2), ∀x1, x2∈R,在複數是否仍然成立。由
sin(z1+z2)=2iei(z1+z2)−e−i(z1+z2)=2ieiz1eiz2−e−iz1e−iz2, 以及
sin(z1)cos(z2)+cos(z1)sin(z2)=2ieiz1−e−iz12eiz2+e−iz2+2eiz1+e−iz12ieiz2−e−iz2=4i1[eiz1eiz2−e−iz1eiz2+eiz1e−iz2−e−iz1e−iz2+eiz1eiz2+e−iz1eiz2−eiz1e−iz2−e−iz1e−iz2]=4i1[eiz1eiz2−e−iz1e−iz2+eiz1eiz2−e−iz1e−iz2]=2ieiz1eiz2−e−iz1e−iz2 因此對任意的 z1, z2∈C,則有 sin(z1+z2)=sin(z1)cos(z2)+cos(z1)sin(z2);同理可得cos(z1+z2)=cos(z1)cos(z2)−sin(z1)sin(z2)。
- 週期性:由前項得知
sin(z+2π)=sin(z)cos(2π)+cos(z)sin(2π)=sin(z),cos(z+2π)=cos(z)cos(2π)−sin(z)sin(2π)=cos(z). 即 sin(z) 與 cos(z) 均為週期等於 2π 之週期函數。同樣展可得對任意的 z∈C,下面關係成立:
{sin(z+π)=−sin(z),cos(z+π)=−cos(z),{sin(z+2π)=cos(z),cos(z+2π)=−sin(z).
- sin(z)=0⟺z=nπ,cos(z)=0⟺z=(n+21)π, n∈Z.
這兩個基本三角函數的映射圖形如下:
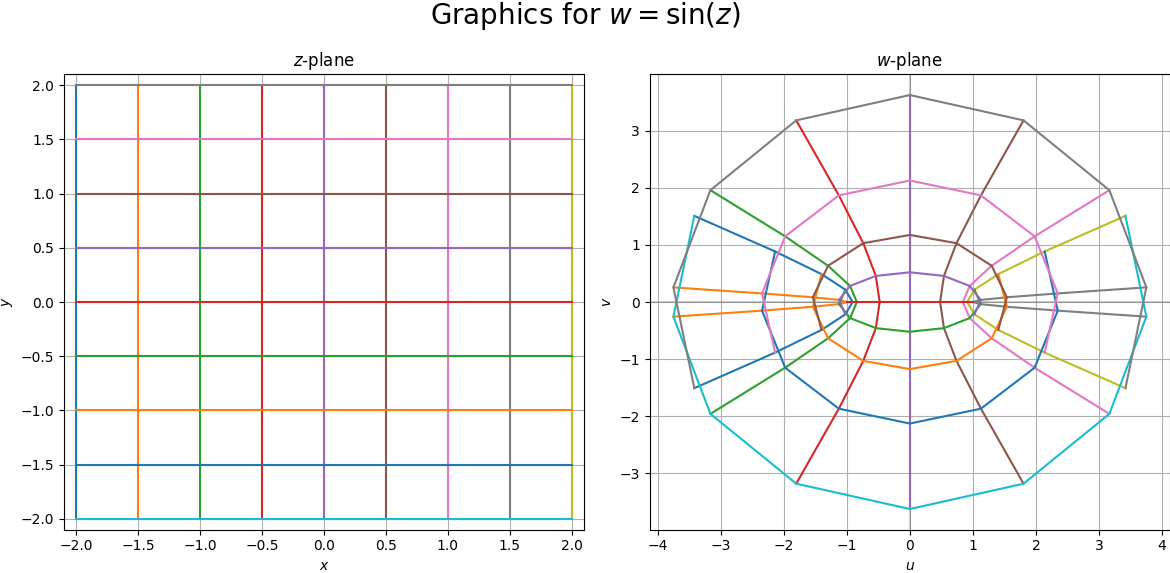

透過修改程式,可以顯示其他三角函數的映射圖形使用的嵌入式python code為:
雙曲函數
複數的雙曲函數定義如下:
定義5.4-2. 令 z∈C,
sinh(z)=2ez−e−z,cosh(z)=2ez+e−z,(5.4-2a) 以及
tanh(z)=cosh(z)sinh(z), coth(z)=sinh(z)cosh(z), sech(z)=cosh(z)1, csch(z)=sinh(z)1.(5.4-2b)
雙曲函數的性質說明如下:
性質
設
z, z1, z2∈C,下列性質成立:
- 導數計算如下:
dzdsinh(z)=2ez+e−z=cosh(z),dzdcosh(z)=2ez−e−z=sinh(z).
- sinh(−z)=2e−z−ez=−sinh(z), cosh(−z)=2e−z+ez=cosh(z)。
- cosh2(z)−sinh2(z)=41[(e2z+2+e−2z)−(e2z−2+e−2z)]=1。
- sinh(z1+z2)=21(ez1ez2−e−z1e−z2),而
sinh(z1)cosh(z2)+cosh(z1)sinh(z2)=2ez1−e−z12ez2+e−z2−2ez1+e−z12ez2−e−z2=4ez1ez2−e−z1ez2+ez1e−z2−e−z1e−z2+ez1ez2+e−z1ez2−ez1e−z2−e−z1e−z2=2ez1ez2−e−z1e−z2 因此 sinh(z1+z2)=sinh(z1)cosh(z2)+cosh(z1)sinh(z2)。
同理可得 cosh(z1+z2)=cosh(z1)cosh(z2)+sinh(z1)sinh(z2)。
- 週期性:由 ei2nπ=1, n∈Z 可得
sinh(z+2πi)=2ezei2π−e−ze−i2π=2ez−e−z=sinh(z),cosh(z+2πi)=2ezei2π+e−ze−i2π=2ez+e−z=cosh(z). 即 sinh(z) 與 cosh(z) 均為週期等於 2πi 之週期函數 (與 ez相同)。
這兩個基本雙曲函數的映射圖形如下:
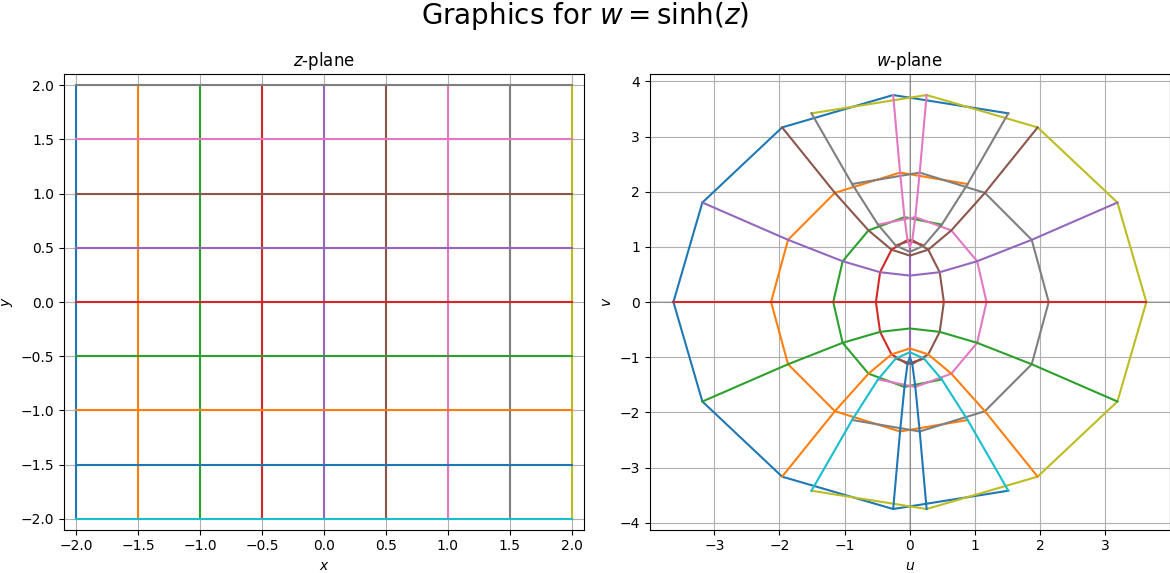

透過修改程式,可以顯示其他三角函數的映射圖形使用的嵌入式python code為:
三角函數和雙曲函數之關係
由於
sin(z)=2ieiz−e−iz,cos(z)=2eiz+e−iz,sinh(z)=2ez−e−z,cosh(z)=2ez+e−z, 可得
cos(z)=cosh(iz),cosh(z)=cos(iz),sin(z)=isinh(iz),sinh(z)=−isin(iz) (or sin(iz)=isinh(z)),(5.4-3) 此外,由
eiz=e−y+ix=e−ycos(x)+ie−ysin(x),e−iz=ey−ix=eycos(x)−ieysin(x), 知
sin(z)=2ieiz−e−iz=cos(x)2ie−y−ey+isin(x)2ie−y+ey,cos(z)=2eiz+e−iz=cos(x)2e−y+ey+isin(x)2e−y−ey, 得
sin(x+iy)=sin(x)cosh(y)+icos(x)sinh(y),cos(x+iy)=cos(x)cosh(y)−isin(x)sinh(y), 另一種推導方式為使用 sin, cos 和差化積,再加上(5.4-3)式的關係可得,即
sin(x+iy)=sin(x)cos(iy)+cos(x)sin(iy)=sin(x)cosh(y)+icos(x)sinh(y),cos(x+iy)=cos(x)cos(iy)−sin(x)sin(iy)=cos(x)cosh(y)−isin(x)sinh(y) 同理可得
sinh(x+iy)=−isin(−y+ix)=sinh(x)cos(y)+icosh(x)sin(y),cosh(x+iy)=cos(−y+ix)=cosh(x)cos(y)+isinh(x)sin(y). 此外,由於
∣sin(x+iy)∣2∣cos(x+iy)∣2=sin2(x)cosh2(y)+cos2(x)sinh2(y)=sin2(x)(cosh2(y)−sinh2(y))+(sin2(x)+cos2(x))sinh2(y)=sin2(x)+sinh2(y),=cos2(x)cosh2(y)+sin2(x)sinh2(y)=cos2(x)(cosh2(y)−sinh2(y))+(sin2(x)+cos2(x))sinh2(y)=cos2(x)+sinh2(y) 以及
∣sinh(x+iy)∣2∣cosh(x+iy)∣2=sinh2(x)+sin2(y),=sinh2(x)+cos2(y), 由於 sinh(x), cosh(x) 為無界函數,得知 sin(z), cos(z), sinh(z), cosh(z) 為無界函數,不像在實數域時 sin(x), cos(x) 的值均落在區間 [−1,1] 之內。



