Newton 迭代法
先回顧求方程式 f ( x ) = 0 f(x)=0 f ( x ) = 0
猜測 x 0 x_0 x 0 計算 x 1 = x 0 − f ( x 0 ) f ′ ( x 0 ) x_1=x_0-\frac{f(x_0)}{f'(x_0)} x 1 = x 0 − f ′ ( x 0 ) f ( x 0 ) 計算 x 2 = x 1 − f ( x 1 ) f ′ ( x 1 ) x_2=x_1-\frac{f(x_1)}{f'(x_1)} x 2 = x 1 − f ′ ( x 1 ) f ( x 1 ) 重複可得 Newton 迭代公式: x n + 1 = x n − f ( x n ) f ′ ( x n ) x_{n+1}=x_{n}-\frac{f(x_n)}{f'(x_n)} x n + 1 = x n − f ′ ( x n ) f ( x n ) n = 2 , 3 , … , n=2,3,\ldots, n = 2 , 3 , … , 計算到當 ∣ x n + 1 − x n ∣ < ε 1 |x_{n+1}-x_{n}|<\varepsilon_1 ∣ x n + 1 − x n ∣ < ε 1 ∣ f ( x n ) ∣ < ε 2 |f(x_n)|<\varepsilon_2 ∣ f ( x n ) ∣ < ε 2 如此一來可以得到一組序列 { x k } k = 0 ∞ = { x 0 , x 1 , x 2 , … , x n , … } \{x_k\}_{k=0}^\infty=\{x_0, x_1, x_2,\ldots, x_n,\ldots\} { x k } k = 0 ∞ = { x 0 , x 1 , x 2 , … , x n , … } { x k } → c \{x_k\}\to c { x k } → c c c c f ( x ) = 0 f(x)=0 f ( x ) = 0 f ( c ) = 0 f(c)=0 f ( c ) = 0
本節的目的就是將這個方法用來求複數方程式 f ( z ) = 0 f(z)=0 f ( z ) = 0
同時所得序列變成 { z k } k = 0 ∞ = { z 0 , z 1 , z 2 , … , z n , … } \{z_k\}_{k=0}^\infty=\{z_0, z_1, z_2,\ldots, z_n,\ldots\} { z k } k = 0 ∞ = { z 0 , z 1 , z 2 , … , z n , … }
範例4.5-1. f ( z ) = z 2 f(z)=z^2 f ( z ) = z 2 z 0 = 1 4 ( 1 + i ) z_0=\frac14(1+i) z 0 = 4 1 ( 1 + i )
[解] 執行五次 Newton 迭代法的結果如下表:
0.25 + 0.25 i 0.25+0.25i 0.25 + 0.25 i 1 + 0.125 i 1+0.125i 1 + 0.125 i − 0.875 + 1.125 i -0.875+1.125i − 0.875 + 1.125 i 0.5 − 1.96875 i 0.5-1.96875i 0.5 − 1.96875 i − 0.222115 + 0.839423 i -0.222115+0.839423i − 0.222115 + 0.839423 i 0.344704 − 0.372898 i 0.344704-0.372898i 0.344704 − 0.372898 i 0.0362403 + 0.976383 i 0.0362403+0.976383i 0.0362403 + 0.976383 i 0.0479896 + 0.0707687 i 0.0479896+0.0707687i 0.0479896 + 0.0707687 i − 0.000861041 + 0.999581 i -0.000861041+0.999581i − 0.000861041 + 0.999581 i 0.000838353 − 0.00172136 i 0.000838353-0.00172136i 0.000838353 − 0.00172136 i 0.0000003606 + 0.999999 i 0.0000003606+0.999999i 0.0000003606 + 0.999999 i 0.0000005668 + 0.0000007212 i 0.0000005668+0.0000007212i 0.0000005668 + 0.0000007212 i
對應圖形如下:
迭代計算時,若執行 k k k f ( z k ) f(z_k) f ( z k ) f ( z ) = 0 f(z)=0 f ( z ) = 0
範例4.5-2. z 0 ∈ R z_0\in\mathbb{R} z 0 ∈ R f ( z ) = z 2 + 1 f(z)=z^2+1 f ( z ) = z 2 + 1
[解] Newton 迭代法的公式為
z n + 1 = z n − z n 2 + 1 2 z n = 1 2 z n − 1 2 z n z_{n+1}=z_n-\frac{z_n^2+1}{2z_n}=\frac{1}{2}z_n-\frac{1}{2z_n} z n + 1 = z n − 2 z n z n 2 + 1 = 2 1 z n − 2 z n 1 因此,當 z 0 ∈ R z_0\in\mathbb{R} z 0 ∈ R 1 2 z 0 , 1 2 z 0 ∈ R \frac{1}{2}z_0,~\frac{1}{2z_0}\in\mathbb{R} 2 1 z 0 , 2 z 0 1 ∈ R z 1 ∈ R z_1\in\mathbb{R} z 1 ∈ R z k ∈ R , ∀ k ≥ 0 z_k\in\mathbb{R},~\forall k\ge 0 z k ∈ R , ∀ k ≥ 0 f ( z ) = z 2 + 1 f(z)=z^2+1 f ( z ) = z 2 + 1 ± i \pm i ± i { z k } \{z_k\} { z k }
Newton 碎形
以下我們討論以求 f ( z ) = z 3 + 1 f(z)=z^3+1 f ( z ) = z 3 + 1 z 3 + 1 = 0 z^3+1=0 z 3 + 1 = 0 − 1 , − ω , − ω 2 -1, ~-\omega, ~-\omega^2 − 1 , − ω , − ω 2 ω 3 = 1 \omega^3=1 ω 3 = 1 z 3 + 1 = 0 z^3+1=0 z 3 + 1 = 0 r 1 = − 1 , r 2 = 1 2 + 3 2 i , r 3 = 1 2 − 3 2 i r_1=-1,~r_2=\frac12+\frac{\sqrt{3}}{2}i, ~r_3=\frac12-\frac{\sqrt{3}}{2}i r 1 = − 1 , r 2 = 2 1 + 2 3 i , r 3 = 2 1 − 2 3 i
設
N ( z ) = z − z 3 + 1 3 z 2 = 2 z 3 − 1 3 z 2 , N(z)=z-\frac{z^3+1}{3z^2}=\frac{2z^3-1}{3z^2}, N ( z ) = z − 3 z 2 z 3 + 1 = 3 z 2 2 z 3 − 1 , 對應的 Newton 迭代法變為 z n + 1 = N ( z n ) z_{n+1}=N(z_n) z n + 1 = N ( z n ) f ( z ) = 0 f(z)=0 f ( z ) = 0 N ( z ) = z N(z)=z N ( z ) = z N ( z ) N(z) N ( z )
計算時先選定包含 f ( z ) = 0 f(z)=0 f ( z ) = 0 R R R R i j R_{ij} R ij z i j z_{ij} z ij
以 z i j z_{ij} z ij N ( z i j ) , N 2 ( z i j ) , N 3 ( z i j ) , … N(z_{ij}),~N^2(z_{ij}),~N^3(z_{ij}), \ldots N ( z ij ) , N 2 ( z ij ) , N 3 ( z ij ) , … N k + 1 ( z ) = N ( N k ( z ) ) N^{k+1}(z)=N(N^{k}(z)) N k + 1 ( z ) = N ( N k ( z )) ε > 0 \varepsilon>0 ε > 0 m > 0 m>0 m > 0 N m ( z i j ) ∈ D ε ( r k ) N^m(z_{ij})\in D_{\varepsilon}(r_k) N m ( z ij ) ∈ D ε ( r k ) N m ( z i j ) N^m(z_{ij}) N m ( z ij ) 將上一步驟的迭代值若收斂接近的根,即使 N m ( z i j ) ∈ D ε ( r k ) N^m(z_{ij})\in D_{\varepsilon}(r_k) N m ( z ij ) ∈ D ε ( r k ) k k k k k k R i j R_{ij} R ij k = 1 , 2 , 3 k=1,~2,~3 k = 1 , 2 , 3 R i j R_{ij} R ij Julia 集合
函數 f ( z ) = z 3 + 1 f(z)=z^3+1 f ( z ) = z 3 + 1 上圖為 f ( z ) = z 3 + 1 f(z)=z^3+1 f ( z ) = z 3 + 1 z 0 z_0 z 0 r 1 = − 1 , r 2 = 1 2 + 3 2 i , r 3 = 1 2 − 3 2 i r_1=-1,~r_2=\frac12+\frac{\sqrt{3}}{2}i, ~r_3=\frac12-\frac{\sqrt{3}}{2}i r 1 = − 1 , r 2 = 2 1 + 2 3 i , r 3 = 2 1 − 2 3 i k ∈ 1 , 2 , 3 k\in{1,2,3} k ∈ 1 , 2 , 3 z n = N n ( z 0 ) z_n=N^n(z_0) z n = N n ( z 0 ) { z n } → r k \{z_n\}\to r_k { z n } → r k
Python 1: Newton 迭代求 z 3 + 1 = 0 z^3+1=0 z 3 + 1 = 0
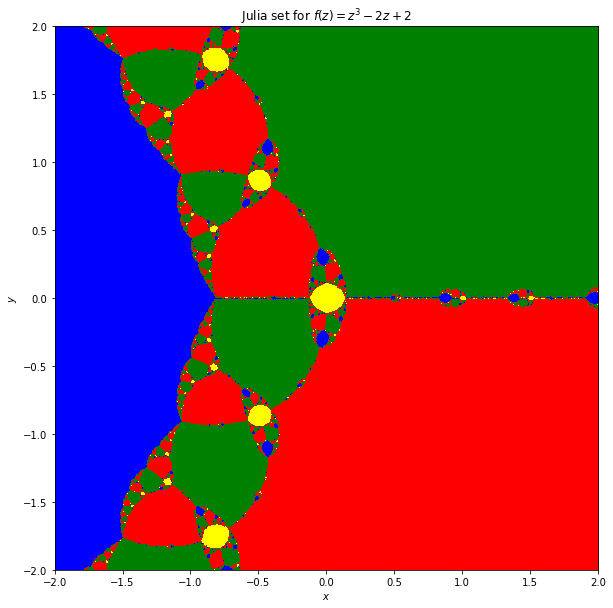
並非對所有的函數進行,所得Julia集合是如上圖沒有黃色的方塊,例如對函數 f ( z ) = z 3 − 2 z + 2 f(z)=z^3-2z+2 f ( z ) = z 3 − 2 z + 2 f ( z ) = 0 f(z)=0 f ( z ) = 0
− 1.7692923542386 , 0.88464617711932 ± 0.589742805022211 i -1.7692923542386,~0.88464617711932 \pm 0.589742805022211i − 1.7692923542386 , 0.88464617711932 ± 0.589742805022211 i 中之任何一個。
函數 f ( z ) = z 3 − 2 z + 2 f(z)=z^3-2z+2 f ( z ) = z 3 − 2 z + 2 二次映射之Julia 集合 Julia 集合是一種分形結構,由法國數學家Gaston Julia 與 Pierre Fatou 於1918發現,這種 Julia 集合不一定要透過 Newton 迭代來產生,換句話說 Julia 集合形成過程可以經由選定複數函數與一個複數作為初始值,並不斷地進行函數的反覆迭代運算 (定點迭代, fixed-point iteration) 來產生。
考慮二次映射:
f c ( z ) = z 2 + c f_c(z) = z^2 + c f c ( z ) = z 2 + c 選定一個複數 z 0 z_0 z 0
z 1 = f c ( z 0 ) , z 2 = f c ( z 1 ) , … , z k + 1 = f c ( z k ) , … z_1=f_c(z_0),~z_2=f_c(z_1),\ldots,z_{k+1}=f_c(z_k),\ldots z 1 = f c ( z 0 ) , z 2 = f c ( z 1 ) , … , z k + 1 = f c ( z k ) , … 探討數列 { z k } \{z_k\} { z k }
範例4.5-3. f c ( z ) = z 2 + c f_c(z)=z^2+c f c ( z ) = z 2 + c c = 0 c=0 c = 0 { z k } \{z_k\} { z k }
[解] 當 c = 0 c=0 c = 0 f 0 ( z ) = z 2 f_0(z)=z^2 f 0 ( z ) = z 2 z 0 = r 0 e i θ 0 z_0=r_0 e^{i\theta_0} z 0 = r 0 e i θ 0 z k = r k e i θ k z_k = r_k e^{i\theta_k} z k = r k e i θ k z k + 1 = f 0 ( z k ) z_{k+1}=f_0(z_k) z k + 1 = f 0 ( z k )
{ r k = r k − 1 2 = r k − 2 4 = ⋯ = r 0 2 k , θ k = 2 θ k − 1 = 4 θ k − 2 = ⋯ = 2 k θ 0 . \begin{cases}
r_{k}&=r_{k-1}^2=r_{k-2}^4=\cdots=r_0^{2^k},\\
\theta_{k}&=2\theta_{k-1}=4\theta_{k-2}=\cdots=2^k \theta_0.
\end{cases} { r k θ k = r k − 1 2 = r k − 2 4 = ⋯ = r 0 2 k , = 2 θ k − 1 = 4 θ k − 2 = ⋯ = 2 k θ 0 . 以下依據 ∣ z 0 ∣ |z_0| ∣ z 0 ∣
∣ z 0 ∣ = r 0 < 1 |z_0|=r_0<1 ∣ z 0 ∣ = r 0 < 1 lim k → ∞ r k = lim k → ∞ r 0 2 k = 0 \lim\limits_{k\to\infty}r_k =\lim\limits_{k\to\infty}r_0^{2^k}=0 k → ∞ lim r k = k → ∞ lim r 0 2 k = 0 { z k } → 0 \{z_k\}\to 0 { z k } → 0 ∣ z 0 ∣ = r 0 = 1 |z_0|=r_0=1 ∣ z 0 ∣ = r 0 = 1 r k = 1 , ∀ k r_k=1,~\forall k r k = 1 , ∀ k θ k = 2 k θ 0 \theta_k=2^k \theta_0 θ k = 2 k θ 0 z k ∈ C 1 ( 0 ) z_k\in C_1(0) z k ∈ C 1 ( 0 ) z k z_k z k n , k n,~k n , k θ 0 = n π / 2 k − 1 \theta_0= n \pi /2^{k-1} θ 0 = nπ / 2 k − 1 { z k } → 1 \{z_k\}\to 1 { z k } → 1 ∣ z 0 ∣ = r 0 > 1 |z_0|=r_0>1 ∣ z 0 ∣ = r 0 > 1 lim k → ∞ r k = lim k → ∞ r 0 2 k = ∞ \lim\limits_{k\to\infty}r_k =\lim\limits_{k\to\infty}r_0^{2^k}=\infty k → ∞ lim r k = k → ∞ lim r 0 2 k = ∞ { z k } → ∞ \{z_k\}\to \infty { z k } → ∞ { z k } \{z_k\} { z k }
定義4.5-1. (軌跡) f c ( z ) = z 2 + c f_c(z)=z^2+c f c ( z ) = z 2 + c z 0 z_0 z 0
z 1 = f c ( z 0 ) , z 2 = f c ( z 1 ) , … , z k + 1 = f c ( z k ) , … z_1=f_c(z_0),~z_2=f_c(z_1),\ldots,z_{k+1}=f_c(z_k),\ldots z 1 = f c ( z 0 ) , z 2 = f c ( z 1 ) , … , z k + 1 = f c ( z k ) , … 所產生的序列 { z k } k = 0 ∞ \{z_k\}_{k=0}^\infty { z k } k = 0 ∞ z 0 z_0 z 0 f c f_c f c 軌跡(orbit) ,並記為 O ( z 0 ; f c ) = { z 0 , z 1 , z 2 , … , z k , … } \mathcal{O}(z_0;f_c)=\{z_0,z_1,z_2,\ldots,z_k,\ldots\} O ( z 0 ; f c ) = { z 0 , z 1 , z 2 , … , z k , … } 。
令 K c K_c K c f c f_c f c z 0 z_0 z 0 z 0 z_0 z 0 範例4.5-3 所對應的 K c K_c K c K 0 = D ‾ 1 ( 0 ) K_0=\overline{D}_1(0) K 0 = D 1 ( 0 ) K c K_c K c f c f_c f c 範例4.5-3 為例, f 0 f_0 f 0 C 1 ( 0 ) C_1(0) C 1 ( 0 )
下圖為 K − 1.25 K_{-1.25} K − 1.25 f − 1.25 f_{-1.25} f − 1.25
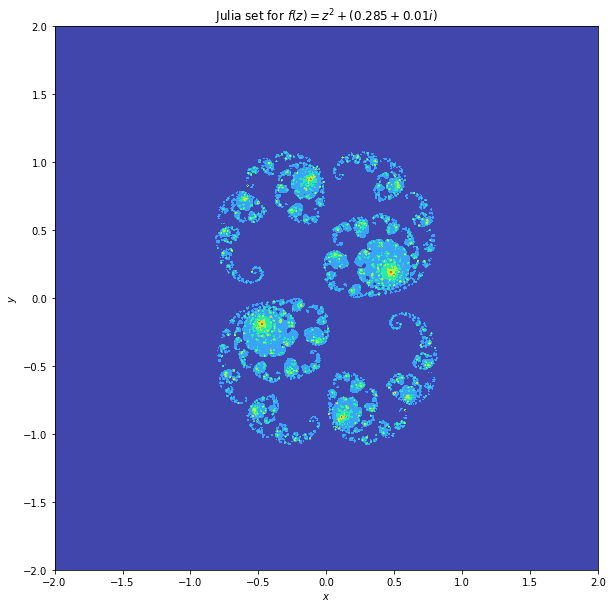
函數 f ( z ) = z 3 − 1.25 f(z)=z^3-1.25 f ( z ) = z 3 − 1.25 Python 2: f ( z ) = z 3 − 1.25 f(z)=z^3-1.25 f ( z ) = z 3 − 1.25 但是對於 f 0.285 + 0.01 i f_{0.285+0.01i} f 0.285 + 0.01 i
函數 f ( z ) = z 3 + 0.286 + 0.01 i f(z)=z^3+0.286+0.01i f ( z ) = z 3 + 0.286 + 0.01 i
定理4.5-1. K c K_c K c 0 ∈ K c 0\in K_c 0 ∈ K c K c K_c K c f c f_c f c f c f_c f c z 0 = 0 z_0=0 z 0 = 0
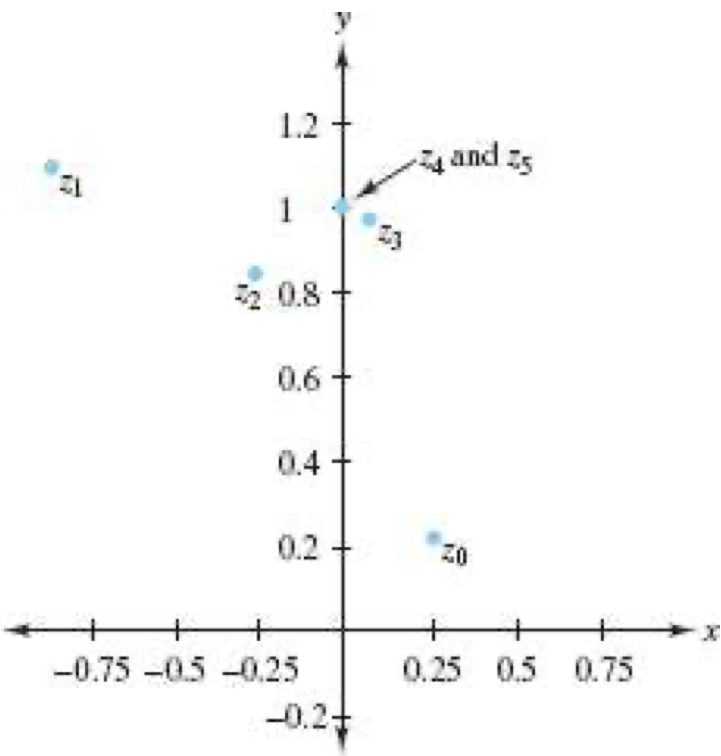
範例4.5-4. f i f_i f i
[解] 討論 z 0 = 0 z_0=0 z 0 = 0
z 1 = f i ( 0 ) = i , z 2 = f i ( i ) = − 1 + i , z 3 = f i ( − 1 + i ) = − i , z 4 = f i ( − i ) = − 1 + i , z 5 = f i ( − 1 + i ) = − i , z 6 = − 1 + i , z 7 = − i , … z_1=f_i(0)=i,~z_2=f_i(i)=-1+i,~z_3 = f_i(-1+i)=-i,\\z_4=f_i(-i)=-1+i,z_5 = f_i(-1+i)=-i,z_6=-1+i,~z_7=-i,\ldots z 1 = f i ( 0 ) = i , z 2 = f i ( i ) = − 1 + i , z 3 = f i ( − 1 + i ) = − i , z 4 = f i ( − i ) = − 1 + i , z 5 = f i ( − 1 + i ) = − i , z 6 = − 1 + i , z 7 = − i , … 因此 z 0 = 0 z_0=0 z 0 = 0 { 0 , i , − 1 + i , − i , − 1 + i , − i , … } \{0,i,-1+i, -i, -1+i, -i, \ldots\} { 0 , i , − 1 + i , − i , − 1 + i , − i , … } f i f_i f i
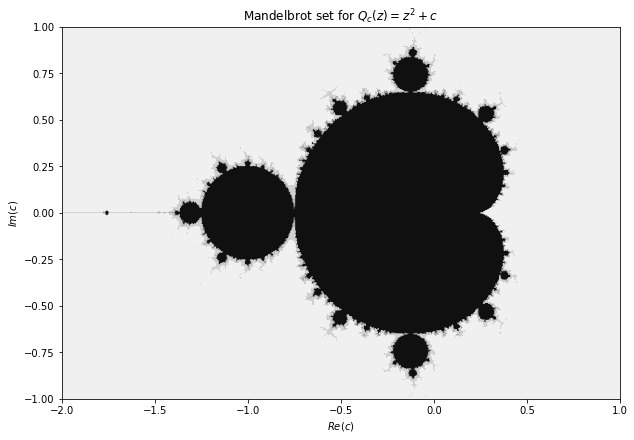
Mandelbrot 集合
在1980年由法國數學家 Benoit Mandelbrot 使用電腦研究
M = { c : f c 的 Julia 集合是連通的 } = { c : f c 進行定點迭代時, z 0 = 0 的軌跡是有界的。 } \begin{align*}
M &= \{ c~:~ f_c \text{的 Julia 集合是連通的}\} \\
&=\{c~:~f_c \text{進行定點迭代時,} z0=0 \text{的軌跡是有界的。}\}
\end{align*} M = { c : f c 的 Julia 集合是連通的 } = { c : f c 進行定點迭代時, z 0 = 0 的軌跡是有界的。 } 此集合 M M M z k z_k z k c c c
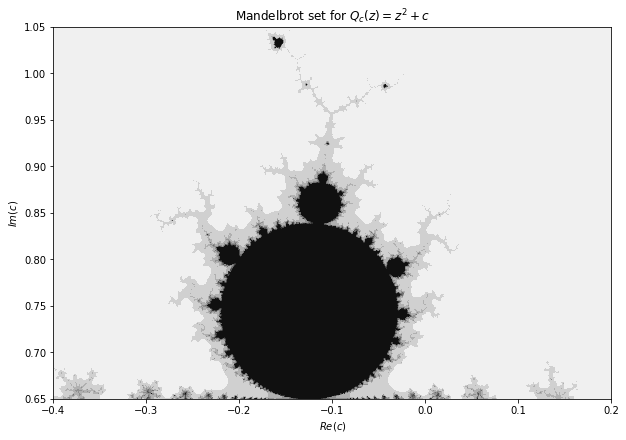
二次函數 c ∈ [ − 2 , 1.0 ] c\in [-2, 1.0] c ∈ [ − 2 , 1.0 ] Python 3: Q c ( z ) = z 2 + c Q_c(z)=z^2+c Q c ( z ) = z 2 + c 調整參數 c c c
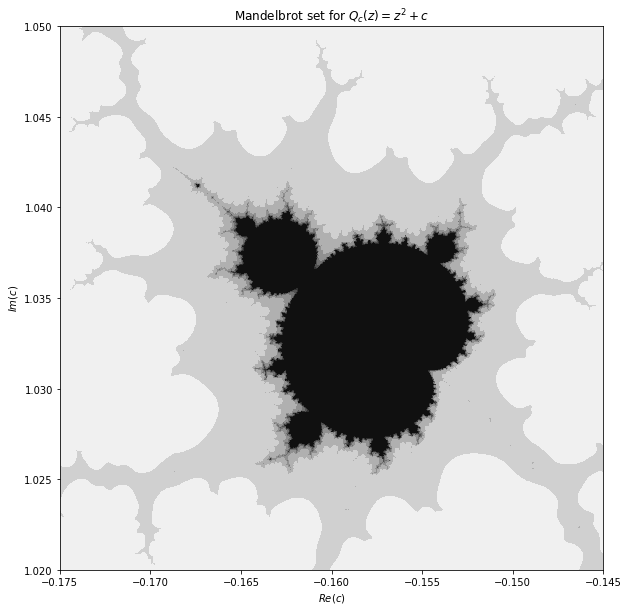
二次函數 c ∈ [ − 0.4 , 0.2 ] c\in[-0.4, 0.2] c ∈ [ − 0.4 , 0.2 ] 二次函數 c ∈ [ − 0.175 , − 0.145 ] c\in [-0.175, -0.145] c ∈ [ − 0.175 , − 0.145 ]
從這三個圖形可以看出當將第一個圖形的上面外凸放大顯示,得到第二個圖形,在將第二個圖形的上邊中間左邊的凸集再放大得到第三個圖形,明顯可以看出第二與三個圖形與第一個圖形類似,再重複放大圖形也會得到相似的結果。這就是所謂的碎形(fractal)結構,即使在無窮小的尺度上,它仍然保持著複雜的結構。
範例4.5-5. O ( 0 , f 1 4 ) \mathcal{O}(0,f_{\frac14}) O ( 0 , f 4 1 )
[解] 對應的迭代式為
z k + 1 = z k 2 + 1 4 , z 0 = 0 , k = 0 , 1 , 2 , … z_{k+1}=z_k^2+\frac14,\quad z_0=0,\quad k=0,1,2,\ldots z k + 1 = z k 2 + 4 1 , z 0 = 0 , k = 0 , 1 , 2 , … 設存在 k k k ∣ z k ∣ ≤ 1 2 |z_k|\le \frac12 ∣ z k ∣ ≤ 2 1
∣ z k + 1 ∣ ≤ ∣ z k ∣ 2 + 1 4 ≤ 1 4 + 1 4 = 1 2 . |z_{k+1}|\le |z_k|^2+\frac14 \le \frac14+\frac14=\frac12. ∣ z k + 1 ∣ ≤ ∣ z k ∣ 2 + 4 1 ≤ 4 1 + 4 1 = 2 1 . 因此由數學歸納法知 ∣ z k ∣ ≤ 1 2 |z_k|\le \frac12 ∣ z k ∣ ≤ 2 1 ∀ k ≥ 0 \forall k\ge 0 ∀ k ≥ 0
∣ z k + 1 z k ∣ 2 = ∣ z k + 1 4 z k ∣ 2 ≥ 4 ∣ z k ∣ ⋅ 1 4 ∣ z k ∣ = 1. \left|\frac{z_{k+1}}{z_k}\right|^2
=\left|z_k+\frac{1}{4z_k}\right|^2\ge 4 |z_k| \cdot \frac{1}{4|z_k|}=1. z k z k + 1 2 = z k + 4 z k 1 2 ≥ 4∣ z k ∣ ⋅ 4∣ z k ∣ 1 = 1. 因此 { ∣ z k ∣ } \{|z_k|\} { ∣ z k ∣ } { ∣ z k ∣ } → 1 2 \{|z_k|\}\to \frac12 { ∣ z k ∣ } → 2 1 z k > 0 z_k>0 z k > 0 ∀ k ≥ 0 \forall k\ge 0 ∀ k ≥ 0 { z k } → 1 2 \{z_k\}\to \frac12 { z k } → 2 1
範例4.5-6. { c : ∣ c ∣ ≤ 1 4 } ⊂ M \{c~:~|c|\le \frac14\}\subset M { c : ∣ c ∣ ≤ 4 1 } ⊂ M
[解] 設 { z k } \{z_k\} { z k } f c ( z ) = z 2 + c f_c(z)=z^2+c f c ( z ) = z 2 + c 0 0 0 ∣ c ∣ ≤ 1 4 |c|\le \frac14 ∣ c ∣ ≤ 4 1
z 0 = 0 , z 1 = f ( z 0 ) = c , z 2 = f ( z 1 ) = c 2 + c , ⋮ z k + 1 = f ( z k ) = z k 2 + c . \begin{align*}
z_0 &= 0, \\
z_1 &= f(z_0) = c,\\
z_2 &= f(z_1) = c^2+c,\\
&\vdots\\
z_{k+1} &= f(z_k)=z_k^2+c.
\end{align*} z 0 z 1 z 2 z k + 1 = 0 , = f ( z 0 ) = c , = f ( z 1 ) = c 2 + c , ⋮ = f ( z k ) = z k 2 + c . Claim: ∣ z k ∣ ≤ 1 2 |z_k|\le \frac12 ∣ z k ∣ ≤ 2 1 k = 0 k=0 k = 0 ∣ z 0 ∣ = 0 ≤ 1 2 |z_0|=0\le \frac12 ∣ z 0 ∣ = 0 ≤ 2 1 k = n k=n k = n ∣ z n ∣ ≤ 1 2 |z_n|\le \frac12 ∣ z n ∣ ≤ 2 1
∣ z n + 1 ∣ = ∣ z n 2 + c ∣ ≤ ∣ z n 2 ∣ + ∣ c ∣ ≤ 1 4 + 1 4 = 1 2 . |z_{n+1}|=|z_n^2+c|\le |z_n^2|+|c|\le\frac14+\frac14=\frac12. ∣ z n + 1 ∣ = ∣ z n 2 + c ∣ ≤ ∣ z n 2 ∣ + ∣ c ∣ ≤ 4 1 + 4 1 = 2 1 . 由數學歸納法得證。因此 { z k } \{z_k\} { z k } { c : ∣ c ∣ ≤ 1 4 } ⊂ M \{c~:~|c|\le \frac14\}\subset M { c : ∣ c ∣ ≤ 4 1 } ⊂ M
類似的作法,可以證明當 ∣ c ∣ > 2 |c|>2 ∣ c ∣ > 2
z 0 = 0 , z 1 = f c ( z 0 ) = c , i.e., ∣ z 1 ∣ = ∣ c ∣ > 2 , z 2 = f c ( z 1 ) = c 2 + c , 且 ∣ z 2 ∣ ∣ z 1 ∣ = ∣ c + 1 c ∣ ≥ ∣ c ∣ − 1 ∣ c ∣ > 2 − 1 2 > 1 , ⋮ z k + 1 = f c ( z k ) = z k 2 + c , 且 ∣ z k + 1 ∣ ∣ z k ∣ = ∣ z k + 1 z k ∣ ≥ ∣ c ∣ − 1 ∣ c ∣ > 1 , \begin{align*}
z_0 &= 0,\\
z_1 &= f_c(z_0)=c,~\text{~i.e.,~}|z_1|=|c|>2,\\
z_2 &= f_c(z_1)=c^2+c,~\text{~且~}\frac{|z_2|}{|z_1|}=\left|c+\frac{1}{c}\right|\ge |c|-\frac{1}{|c|}>2-\frac12>1,\\
&\vdots \\
z_{k+1} &= f_c(z_k)=z_k^2+c,~\text{~且~}\frac{|z_{k+1}|}{|z_{k}|}=\left|z_k+\frac{1}{z_k}\right|\ge |c|-\frac{1}{|c|}>1,
\end{align*} z 0 z 1 z 2 z k + 1 = 0 , = f c ( z 0 ) = c , i.e., ∣ z 1 ∣ = ∣ c ∣ > 2 , = f c ( z 1 ) = c 2 + c , 且 ∣ z 1 ∣ ∣ z 2 ∣ = c + c 1 ≥ ∣ c ∣ − ∣ c ∣ 1 > 2 − 2 1 > 1 , ⋮ = f c ( z k ) = z k 2 + c , 且 ∣ z k ∣ ∣ z k + 1 ∣ = z k + z k 1 ≥ ∣ c ∣ − ∣ c ∣ 1 > 1 , 因此 { ∣ z k ∣ } \{|z_{k}|\} { ∣ z k ∣ } O ( 0 , f c ) \mathcal{O}(0,f_c) O ( 0 , f c ) c ∉ M c\not\in M c ∈ M
範例4.5-7. O ( z 0 , f − 2 ) \mathcal{O}(z_0,f_{-2}) O ( z 0 , f − 2 )
[解] 設 z k ∈ O ( z 0 , f − 2 ) z_k\in\mathcal{O}(z_0,f_{-2}) z k ∈ O ( z 0 , f − 2 )
z k + 1 = z k 2 − 2 , z 0 = 0 , k = 0 , 1 , 2 , … z_{k+1}=z_k^2-2,\quad z_0=0,\quad k=0,1,2,\ldots z k + 1 = z k 2 − 2 , z 0 = 0 , k = 0 , 1 , 2 , … 依據 z k z_k z k
設存在 k k k ∣ z k ∣ > 2 |z_k|>2 ∣ z k ∣ > 2 ∣ z k + 1 ∣ = ∣ z k 2 − 2 ∣ 2 ≥ ∣ z k ∣ 2 − 2 > 2 2 − 2 = 2 |z_{k+1}|=|z_k^2-2|^2\ge |z_k|^2-2>2^2-2=2 ∣ z k + 1 ∣ = ∣ z k 2 − 2 ∣ 2 ≥ ∣ z k ∣ 2 − 2 > 2 2 − 2 = 2 ∣ z n ∣ > 2 , ∀ n ≥ k |z_n|>2,~\forall n\ge k ∣ z n ∣ > 2 , ∀ n ≥ k ∣ z k + 1 z k ∣ = ∣ z k − 2 z k ∣ ≥ ∣ z k ∣ − ∣ 2 z k ∣ > 2 − 1 = 1 , \left|\frac{z_{k+1}}{z_k}\right|=\left|z_k-\frac{2}{z_k}\right|\ge |z_k|-\left|\frac{2}{z_k}\right|>2-1=1, z k z k + 1 = z k − z k 2 ≥ ∣ z k ∣ − z k 2 > 2 − 1 = 1 , 所以 { ∣ z k ∣ } \{|z_k|\} { ∣ z k ∣ } ∞ \infty ∞ O ( z 0 , f − 2 ) \mathcal{O}(z_0,f_{-2}) O ( z 0 , f − 2 )
設存在 k k k ∣ z k ∣ = 2 |z_k|=2 ∣ z k ∣ = 2 z k = 2 e i θ z_k=2 e^{i\theta} z k = 2 e i θ 則有
∣ z k + 1 ∣ 2 = ( 4 cos ( 2 θ ) − 2 ) 2 + 16 sin 2 ( 2 θ ) = 20 − 16 cos 2 θ ≥ 20 − 16 = 4 , |z_{k+1}|^2=(4\cos(2\theta)-2)^2+16\sin^2(2\theta)=20-16\cos2\theta\ge 20-16=4, ∣ z k + 1 ∣ 2 = ( 4 cos ( 2 θ ) − 2 ) 2 + 16 sin 2 ( 2 θ ) = 20 − 16 cos 2 θ ≥ 20 − 16 = 4 , 亦即 ∣ z k + 1 ∣ ≥ 2 |z_{k+1}|\ge 2 ∣ z k + 1 ∣ ≥ 2 θ = n π \theta=n\pi θ = nπ z k = − 2 , 2 z_k=-2,2 z k = − 2 , 2 z n = 2 , ∀ n ≥ k + 1 z_{n}=2,~\forall n\ge k+1 z n = 2 , ∀ n ≥ k + 1 O ( z 0 , f − 2 ) → 2 \mathcal{O}(z_0,f_{-2})\to 2 O ( z 0 , f − 2 ) → 2 θ ≠ n π \theta\neq n\pi θ = nπ ∣ z k + 1 ∣ > 2 |z_{k+1}|>2 ∣ z k + 1 ∣ > 2 O ( z 0 , f − 2 ) \mathcal{O}(z_0,f_{-2}) O ( z 0 , f − 2 )
設存在 k k k ∣ z k ∣ < 2 |z_k|<2 ∣ z k ∣ < 2 z k = 0 z_k=0 z k = 0 z k = − 1 z_k=-1 z k = − 1 z k = x k ∈ R z_k=x_k\in\mathbb{R} z k = x k ∈ R z k = i y k ∈ I z_k=i y_k\in\mathbb{I} z k = i y k ∈ I z k = 0 z_k=0 z k = 0 z k + 1 = z k 2 − 2 = − 2 z_{k+1}=z_k^2-2=-2 z k + 1 = z k 2 − 2 = − 2 O ( z 0 , f − 2 ) → 2 \mathcal{O}(z_0,f_{-2})\to 2 O ( z 0 , f − 2 ) → 2 z k = − 1 z_k=-1 z k = − 1 z k + 1 = z k 2 − 2 = − 1 z_{k+1}=z_k^2-2=-1 z k + 1 = z k 2 − 2 = − 1 O ( z 0 , f − 2 ) → − 1 \mathcal{O}(z_0,f_{-2})\to -1 O ( z 0 , f − 2 ) → − 1 z k = x k ∈ R z_k=x_k\in\mathbb{R} z k = x k ∈ R O ( z 0 , f − 2 ) \mathcal{O}(z_0,f_{-2}) O ( z 0 , f − 2 ) x x x z k + 1 = x k 2 − 2 ∈ R z_{k+1}=x_k^2-2\in\mathbb{R} z k + 1 = x k 2 − 2 ∈ R O ( z 0 , f − 2 ) ⊂ R \mathcal{O}(z_0,f_{-2})\subset \mathbb{R} O ( z 0 , f − 2 ) ⊂ R x k 2 = 2 x_k^2=2 x k 2 = 2 z k + 1 = 0 z_{k+1}=0 z k + 1 = 0 O ( z 0 , f − 2 ) → 2 \mathcal{O}(z_0,f_{-2})\to 2 O ( z 0 , f − 2 ) → 2 z k = i y k , y k ∈ R z_k=iy_k,~y_k\in\mathbb{R} z k = i y k , y k ∈ R z k + 1 = − y k 2 − 2 < − 2 z_{k+1}=-y_k^2-2 < -2 z k + 1 = − y k 2 − 2 < − 2 z k + 1 ∈ R z_{k+1}\in\mathbb{R} z k + 1 ∈ R ∣ z k + 1 ∣ > 2 |z_{k+1}|>2 ∣ z k + 1 ∣ > 2 z k + 2 = z k + 1 2 + 2 − 2 = ( y k 2 + 2 ) 2 − 2 = y k 4 + 4 y k 2 + 2 > 2 z_{k+2}=z_{k+1}^2+2-2=(y_k^2+2)^2-2=y_k^4+4y_k^2+2>2 z k + 2 = z k + 1 2 + 2 − 2 = ( y k 2 + 2 ) 2 − 2 = y k 4 + 4 y k 2 + 2 > 2 也就是說 z n ∈ R , n ≥ k + 2 z_n\in\mathbb{R},~n\ge k+2 z n ∈ R , n ≥ k + 2 O ( z 0 , f − 2 ) \mathcal{O}(z_0,f_{-2}) O ( z 0 , f − 2 ) ∞ \infty ∞
由範例4.5-7 O ( 0 , f − 2 ) → 2 \mathcal{O}(0,f_{-2})\to 2 O ( 0 , f − 2 ) → 2 − 2 ∈ M -2\in M − 2 ∈ M C 2 ( 0 ) ∩ M ≠ ∅ C_2(0)\cap M\neq \empty C 2 ( 0 ) ∩ M = ∅ M M M D ‾ 1 4 ( 0 ) ⊂ M ⊂ D ‾ 2 ( 0 ) \overline{D}_\frac14(0)\subset M\subset \overline{D}_2(0) D 4 1 ( 0 ) ⊂ M ⊂ D 2 ( 0 )
下圖說明 Mandelbrot 集合上的 c c c
進一步分析 Mandelbrot 集合
定義4.5-2. (定點、不動點) F ( α ) = α F(\alpha)=\alpha F ( α ) = α α \alpha α F F F 定點 或 不動點 ( fixed point ) 。
定義4.5-3. (吸引點) ∣ F ′ ( α ) ∣ < 1 |F'(\alpha)|<1 ∣ F ′ ( α ) ∣ < 1 α \alpha α F F F 吸引點 ( attracting point ),而當 ∣ F ′ ( α ) ∣ > 1 |F'(\alpha)|>1 ∣ F ′ ( α ) ∣ > 1 α \alpha α F F F 排斥點 ( pelling point ), 。
範例4.5-8. F ( z ) = z 2 − z + 1 F(z)=z^2-z+1 F ( z ) = z 2 − z + 1 z = 1 z=1 z = 1 F F F F ( 1 ) = 1 2 − 1 + 1 = 1 F(1)=1^2-1+1=1 F ( 1 ) = 1 2 − 1 + 1 = 1 F ′ ( z ) = 2 z − 3 F'(z)=2z-3 F ′ ( z ) = 2 z − 3 F ′ ( 1 ) = 2 − 3 = − 1 F'(1)=2-3=-1 F ′ ( 1 ) = 2 − 3 = − 1 z = 1 z=1 z = 1
並非所有函數都有不動點,例如 F ( z ) = z + 1 F(z)=z+1 F ( z ) = z + 1 z + 1 ≠ z z+1\neq z z + 1 = z
定點的說明透過實數比較清楚,給定實函數 y = f ( x ) y=f(x) y = f ( x ) f f f y = f ( x ) y=f(x) y = f ( x ) y = x y=x y = x L r ( x ) = r x ( 1 − x ) L_r(x)=r x (1-x) L r ( x ) = r x ( 1 − x ) x = 0 x=0 x = 0 x = 1 − 1 r x=1-\frac1{r} x = 1 − r 1 L r ′ ( x ) = r ( 1 − 2 x ) L_r'(x)=r(1-2x) L r ′ ( x ) = r ( 1 − 2 x ) L r ′ ( 0 ) = r L_r'(0)=r L r ′ ( 0 ) = r L r ′ ( 1 − 1 r ) = 2 − r L_r'(1-\frac1{r})=2-r L r ′ ( 1 − r 1 ) = 2 − r r ∈ [ 0 , 4 ] r\in[0,4] r ∈ [ 0 , 4 ]
下面為Geogebra的圖示,可以拉動滑桿,觀察 r r r
Geogebra 1: L ( x ) = r x ( 1 − x ) L(x)=r x (1-x) L ( x ) = r x ( 1 − x )
同樣地,二次函數 f c ( x ) = x 2 + c f_c(x)=x^2+c f c ( x ) = x 2 + c
Geogebra 2: f c ( x ) = x 2 + c f_c(x)=x^2+c f c ( x ) = x 2 + c
定理4.5-2. α \alpha α F F F D r ( α ) D_r(\alpha) D r ( α ) z 0 ∈ D r ∗ ( α ) z_0\in D_r^*(\alpha) z 0 ∈ D r ∗ ( α ) α \alpha α z ∈ D r ∗ ( α ) z\in D_r^*(\alpha) z ∈ D r ∗ ( α ) ∣ F ( z ) − α ∣ < ∣ z − α ∣ |F(z)-\alpha|<|z-\alpha| ∣ F ( z ) − α ∣ < ∣ z − α ∣ z k ∈ O ( z 0 , F ) z_k\in\mathcal{O}(z_0,F) z k ∈ O ( z 0 , F ) lim k → ∞ z k = α \lim\limits_{k\to \infty}z_k =\alpha k → ∞ lim z k = α
[證明] (第一部份) 因 α \alpha α F F F ∣ F ′ ( α ) ∣ < 1 |F'(\alpha)|<1 ∣ F ′ ( α ) ∣ < 1 F F F α \alpha α
選定 ε = 1 − ∣ F ′ ( α ) ∣ \varepsilon = 1-|F'(\alpha)| ε = 1 − ∣ F ′ ( α ) ∣ z ∈ D r ∗ ( α ) z\in D_r^*(\alpha) z ∈ D r ∗ ( α )
∣ F ( z ) − F ( α ) z − α ∣ − ∣ F ′ ( α ) ∣ ≤ ∣ F ( z ) − F ( α ) z − α − F ′ ( α ) ∣ < 1 − ∣ F ′ ( α ) ∣ . \left|\frac{F(z)-F(\alpha)}{z-\alpha}\right|-\left|F'(\alpha)\right|\le \left|\frac{F(z)-F(\alpha)}{z-\alpha}-F'(\alpha)\right|<1-|F'(\alpha)|. z − α F ( z ) − F ( α ) − ∣ F ′ ( α ) ∣ ≤ z − α F ( z ) − F ( α ) − F ′ ( α ) < 1 − ∣ F ′ ( α ) ∣. 亦即
∣ F ( z ) − F ( α ) z − α ∣ < 1 ⟹ ∣ F ( z ) − F ( α ) ∣ = ∣ F ( z ) − α ∣ < ∣ z − α ∣ . \left|\frac{F(z)-F(\alpha)}{z-\alpha}\right|<1\implies |F(z)-F(\alpha)|=|F(z)-\alpha|<|z-\alpha|. z − α F ( z ) − F ( α ) < 1 ⟹ ∣ F ( z ) − F ( α ) ∣ = ∣ F ( z ) − α ∣ < ∣ z − α ∣. (第二部份) 設 z k ∈ O ( z 0 , F ) z_k\in\mathcal{O}(z_0,F) z k ∈ O ( z 0 , F )
∣ z k + 1 − α ∣ = ∣ F ( z k ) − α ∣ < ∣ z k − α ∣ , ∀ k ≥ 0 |z_{k+1}-\alpha|=|F(z_k)-\alpha|<|z_k-\alpha|,\quad \forall k\ge 0 ∣ z k + 1 − α ∣ = ∣ F ( z k ) − α ∣ < ∣ z k − α ∣ , ∀ k ≥ 0 因此 { ∣ z k − α ∣ } \{|z_k-\alpha|\} { ∣ z k − α ∣ } { ∣ z k − α ∣ } → 0 \{|z_k-\alpha|\}\to0 { ∣ z k − α ∣ } → 0 lim k → ∞ ∣ z k − α ∣ = 0 \lim\limits_{k\to \infty}|z_k-\alpha| =0 k → ∞ lim ∣ z k − α ∣ = 0 lim k → ∞ z k = α \lim\limits_{k\to\infty}z_k=\alpha k → ∞ lim z k = α ■ \hspace{0.1cm}\blacksquare ■
1905年 Fatou 證明有些二次函數 f c ( z ) = z 2 + c f_c(z)=z^2+c f c ( z ) = z 2 + c O ( 0 , f c ) \mathcal{O}(0,f_c) O ( 0 , f c ) M M M c c c M M M c c c
定理4.5-3. f c ( z ) = z 2 + c f_c(z)=z^2+c f c ( z ) = z 2 + c ∣ 1 + 1 − 4 c ∣ < 1 |1+\sqrt{1-4c}|<1 ∣1 + 1 − 4 c ∣ < 1 ∣ 1 − 1 − 4 c ∣ < 1 |1-\sqrt{1-4c}|<1 ∣1 − 1 − 4 c ∣ < 1 a \sqrt{\phantom{a}} a
[證明] 設點 α \alpha α f c f_c f c α \alpha α α 2 − α + c = 0 \alpha^2-\alpha+c=0 α 2 − α + c = 0 α = 1 ± 1 − 4 c 2 \alpha=\frac{1\pm \sqrt{1-4c}}{2} α = 2 1 ± 1 − 4 c α \alpha α ∣ f c ′ ( α ) ∣ = ∣ 2 α ∣ < 1 |f_c'(\alpha)|=|2\alpha|<1 ∣ f c ′ ( α ) ∣ = ∣2 α ∣ < 1 ∣ α ∣ < 1 |\alpha|<1 ∣ α ∣ < 1 ∣ 1 + 1 − 4 c ∣ < 1 |1+\sqrt{1-4c}|<1 ∣1 + 1 − 4 c ∣ < 1 ∣ 1 − 1 − 4 c ∣ < 1 |1-\sqrt{1-4c}|<1 ∣1 − 1 − 4 c ∣ < 1
定義4.5-4. (n週期) F F F n週期 n-cycle { z 0 , z 1 , … , z n − 1 } \{z_0,z_1,\ldots,z_{n-1}\} { z 0 , z 1 , … , z n − 1 } z k = F ( z k − 1 , 1 ≤ k ≤ n − 1 z_k=F(z_{k-1},~1\le k\le n-1 z k = F ( z k − 1 , 1 ≤ k ≤ n − 1 F ( z n − 1 ) = z 0 F(z_{n-1})=z_0 F ( z n − 1 ) = z 0
定義4.5-5. (吸性n週期) g n g_n g n F F F n n n g 2 ( z ) = ( F ∘ F ) ( z ) = F ( F ( z ) ) g_2(z) = (F\circ F)(z)=F(F(z)) g 2 ( z ) = ( F ∘ F ) ( z ) = F ( F ( z )) ∣ g n ′ ( z 0 ) ∣ < 1 |g_n'(z_0)|<1 ∣ g n ′ ( z 0 ) ∣ < 1 F F F n週期 (n-cycle) { z 0 , z 1 , … , z n − 1 } \{z_0,z_1,\ldots,z_{n-1}\} { z 0 , z 1 , … , z n − 1 } 吸引n週期 attracting n-cycle
範例4.5-9. 範例4.5-4 f i f_i f i
[解] 由函數 f i f_i f i { 0 , i , − 1 + i , − i , − 1 + i , − i , … } \{0,i,-1+i, -i, -1+i, -i, \ldots\} { 0 , i , − 1 + i , − i , − 1 + i , − i , … } { − 1 + i , − i } \{-1+i, -i\} { − 1 + i , − i } { − i , − 1 + i } \{-i, -1+i\} { − i , − 1 + i }
因此 g 2 ′ ( z ) = 4 z 3 + 4 i z g_2'(z)=4z^3+4iz g 2 ′ ( z ) = 4 z 3 + 4 i z g 2 ′ ( − 1 + i ) = g 2 ′ ( − i ) = 4 + 4 i g_2'(-1+i)=g_2'(-i)=4+4i g 2 ′ ( − 1 + i ) = g 2 ′ ( − i ) = 4 + 4 i ∣ g 2 ′ ( − 1 + i ) ∣ = ∣ g 2 ′ ( i ) ∣ = ∣ 4 + 4 i ∣ > 1 |g_2'(-1+i)|=|g_2'(i)|=|4+4i|>1 ∣ g 2 ′ ( − 1 + i ) ∣ = ∣ g 2 ′ ( i ) ∣ = ∣4 + 4 i ∣ > 1 { − 1 + i , − i } \{-1+i, -i\} { − 1 + i , − i } f i f_i f i z 0 = − i + 0.1 z_0=-i+0.1 z 0 = − i + 0.1 O ( z 0 ; f i ) \mathcal{O}(z_0;f_i) O ( z 0 ; f i )
相關影片
總結
Julia 集合與 Mandelbrot 集合都是數學中引人入勝的分碎形結構,它們各自展示了令人驚嘆的自相似性和複雜性。這兩種集合雖有各自的特點,但它們共享一些基本的數學性質,尤其是在自相似性和從簡單規則中產生複雜結構的能力方面。
Julia 集合以其在任何尺度下局部結構與整體結構相似的特性著稱。這意味著無論我們如何放大或縮小它,都能觀察到相似的形狀和結構。這種特性賦予了 Julia 集合一種視覺上的無窮複雜性,使其成為數學和藝術領域中的重要研究對象。Julia 集合的這種高度複雜性源於一個相對簡單的迭代公式,透過無窮次的迭代,產生出極度複雜的形狀和結構,展現了碎形理論中從簡單規則產生複雜性的核心特徵。
與此同時,Mandelbrot 集合在複數平面上形成的結構同樣展示了驚人的複雜性和對稱美。其碎形邊界上的每一部分都以某種方式反映出整體的形狀,呈現出碎形結構的無窮複雜性。 Mandelbrot 集合的簡單數學定義與其所揭示的深奧數學性質如混沌和自相似性形成鮮明對比,使其成為了動態系統理論的重要研究對象。
在數學領域,Julia 集合和 Mandelbrot 集合都被用來研究複數系統的動態行為和複雜系統的混沌現象。它們幫助我們理解從簡單的數學規則中如何產生出複雜的行為模式。而在藝術領域,這兩種集合的視覺效果引起了廣泛關注。它們的豐富色彩和無窮複雜性使其成為獨特的視覺藝術形式,吸引了眾多藝術家和設計師利用計算機技術將其結構視覺化,並應用於各種藝術作品和設計中。
習題
考慮函數 f ( z ) = z 2 + 1 f(z)=z^2+1 f ( z ) = z 2 + 1 N ( z ) = 1 2 ( z − 1 z ) N(z)=\frac12(z-\frac1{z}) N ( z ) = 2 1 ( z − z 1 ) z k + 1 = N ( z k ) , k = 0 , 1 , 2 , … z_{k+1}=N(z_k),~k=0,1,2,\ldots z k + 1 = N ( z k ) , k = 0 , 1 , 2 , … { z k } \{z_k\} { z k } 證明若 Im ( z 0 ) > 0 \text{Im}(z_0)>0 Im ( z 0 ) > 0 { z k } \{z_k\} { z k } Im ( z k ) > 0 , ∀ k ≥ 0 \text{Im}(z_k)>0,~\forall k\ge 0 Im ( z k ) > 0 , ∀ k ≥ 0 Im ( z 0 ) < 0 \text{Im}(z_0)<0 Im ( z 0 ) < 0 Im ( z k ) < 0 , ∀ k ≥ 0 \text{Im}(z_k)<0,~\forall k\ge 0 Im ( z k ) < 0 , ∀ k ≥ 0 [解] 若 Im ( z k ) > 0 \text{Im}(z_k)>0 Im ( z k ) > 0 Im ( 1 z k ) = Im ( z ˉ k ∣ z k ∣ 2 ) < 0 \text{Im}\left(\frac{1}{z_k}\right)=\text{Im}\left(\frac{\bar{z}_k}{|z_k|^2}\right)<0 Im ( z k 1 ) = Im ( ∣ z k ∣ 2 z ˉ k ) < 0 z k + 1 = 1 2 ( z k − 1 z k ) z_{k+1}=\frac12(z_k-\frac{1}{z_k}) z k + 1 = 2 1 ( z k − z k 1 ) Im ( z k + 1 ) > 0 \text{Im}(z_{k+1})>0 Im ( z k + 1 ) > 0 Im ( z k ) > 0 , ∀ k ≥ 0 \text{Im}(z_k)>0,~\forall k\ge 0 Im ( z k ) > 0 , ∀ k ≥ 0 Im ( z 0 ) < 0 \text{Im}(z_0)<0 Im ( z 0 ) < 0 Im ( z k ) < 0 , ∀ k ≥ 0 \text{Im}(z_k)<0,~\forall k\ge 0 Im ( z k ) < 0 , ∀ k ≥ 0
當 z 0 ∈ R z_0\in\mathbb{R} z 0 ∈ R { z k } ⊂ R \{z_k\}\subset \mathbb{R} { z k } ⊂ R 討論當 Im ( z 0 ) > 0 \text{Im}(z_0)>0 Im ( z 0 ) > 0 { z k } \{z_k\} { z k } i i i Im ( z 0 ) < 0 \text{Im}(z_0)<0 Im ( z 0 ) < 0 { z k } \{z_k\} { z k } − i -i − i 請嘗試精細描述 K − 2 K_{-2} K − 2 請證明下列與集合 M M M 若 c ∈ M c\in M c ∈ M c ‾ ∈ M \overline{c}\in M c ∈ M [解] 若 c ∈ M c\in M c ∈ M z k + 1 = z k 2 + c , k = 0 , 1 , 2 , … z_{k+1}=z_k^2+c,\quad k=0,1,2,\ldots z k + 1 = z k 2 + c , k = 0 , 1 , 2 , … O ( 0 , f c ) = { 0 , z 1 , z 2 , z 3 , … } \mathcal{O}(0,f_c)=\{0,z_1,z_2,z_3,\ldots\} O ( 0 , f c ) = { 0 , z 1 , z 2 , z 3 , … } ∃ M > 0 \exists M>0 ∃ M > 0 ∣ z k ∣ ≤ M |z_k|\le M ∣ z k ∣ ≤ M z ˉ k + 1 = z ˉ k 2 + c ˉ , z ˉ 0 = 0 , k = 0 , 1 , 2 , … \bar{z}_{k+1}=\bar{z}_k^2+\bar{c},~\bar{z}_0=0, \quad k=0,1,2,\ldots z ˉ k + 1 = z ˉ k 2 + c ˉ , z ˉ 0 = 0 , k = 0 , 1 , 2 , … ∣ z ˉ k ∣ ≤ M |\bar{z}_k|\le M ∣ z ˉ k ∣ ≤ M O ( 0 , f c ˉ ) = { 0 , z ˉ 1 , z ˉ 2 , z ˉ 3 , … } \mathcal{O}(0,f_{\bar{c}})=\{0,\bar{z}_1,\bar{z}_2,\bar{z}_3,\ldots\} O ( 0 , f c ˉ ) = { 0 , z ˉ 1 , z ˉ 2 , z ˉ 3 , … } c ‾ ∈ M \overline{c}\in M c ∈ M
請證明若 c ∈ R c\in \mathbb{R} c ∈ R c > 1 4 c>\frac14 c > 4 1 c ∉ M c\not\in M c ∈ M [解] 若 c ∈ R c\in \mathbb{R} c ∈ R c > 1 4 c>\frac14 c > 4 1
即 z k > 0 , ∀ n ≥ 1 z_k>0,~\forall n\ge 1 z k > 0 , ∀ n ≥ 1
Claim: ∣ z k ∣ > 1 4 , ∀ n ≥ 1 |z_{k}|>\frac14,~\forall n\ge 1 ∣ z k ∣ > 4 1 , ∀ n ≥ 1
明顯 k = 0 k=0 k = 0 k = n k=n k = n ∣ z n ∣ > 1 4 |z_n|>\frac14 ∣ z n ∣ > 4 1 k = n + 1 k=n+1 k = n + 1
z n + 1 = z n 2 + c > ( 1 4 ) 2 + 1 4 > 1 4 z_{n+1}=z_n^2+c>\left(\frac14\right)^2+\frac14>\frac14 z n + 1 = z n 2 + c > ( 4 1 ) 2 + 4 1 > 4 1 由數學歸納法得證。
Claim: { z k } \{z_{k}\} { z k } z k + 1 z k > 1 , ∀ n ≥ 1 \frac{z_{k+1}}{z_k}>1,~\forall n\ge 1 z k z k + 1 > 1 , ∀ n ≥ 1
由算幾不等式知當 k > 1 k>1 k > 1
z k + 1 z k = z k + c z k ≥ 2 z k ⋅ c z k = 2 c > 1 \frac{z_{k+1}}{z_k}=z_k+\frac{c}{z_k}\ge 2\sqrt{z_k\cdot \frac{c}{z_k}}=2\sqrt{c}>1 z k z k + 1 = z k + z k c ≥ 2 z k ⋅ z k c = 2 c > 1 即 { z k } \{z_{k}\} { z k }
由於 { z k } \{z_{k}\} { z k } lim k → ∞ z k = ∞ \lim\limits_{k\to\infty} z_k=\infty k → ∞ lim z k = ∞ O ( 0 , f c ) \mathcal{O}(0,f_c) O ( 0 , f c ) c ∉ M c\not\in M c ∈ M
z 1 = 0 , z 1 = c , z 2 = c 2 + c , … , z k + 1 = z k 2 + c , … z_1=0,z_1=c, z_2=c^2+c,\ldots, z_{k+1}=z_{k}^2+c, \ldots z 1 = 0 , z 1 = c , z 2 = c 2 + c , … , z k + 1 = z k 2 + c , … 證明若 c c c ∣ 1 + 1 − 4 c ∣ < 1 |1+\sqrt{1-4c}|<1 ∣1 + 1 − 4 c ∣ < 1 ∣ 1 − 1 − 4 c ∣ < 1 |1-\sqrt{1-4c}|<1 ∣1 − 1 − 4 c ∣ < 1 [解] 邊界為 ∣ 1 ± 1 − 4 c ∣ = 1 |1\pm\sqrt{1-4c}|=1 ∣1 ± 1 − 4 c ∣ = 1 1 ± 1 − 4 c = e i θ 1\pm\sqrt{1-4c}=e^{i\theta} 1 ± 1 − 4 c = e i θ
± 1 − 4 c = e i θ − 1 ⟺ 1 − 4 c = ( e i θ − 1 ) 2 = 1 − 2 e i θ − e i 2 θ ⟺ c = 1 2 e i θ + 1 4 e i 2 θ \begin{align*}
\pm \sqrt{1-4c} = e^{i\theta}-1
&\iff
1-4c = (e^{i\theta}-1)^2=1-2e^{i\theta}-e^{i2\theta} \\
&\iff
c = \frac12 e^{i\theta}+\frac14 e^{i2\theta}
\end{align*} ± 1 − 4 c = e i θ − 1 ⟺ 1 − 4 c = ( e i θ − 1 ) 2 = 1 − 2 e i θ − e i 2 θ ⟺ c = 2 1 e i θ + 4 1 e i 2 θ 因此
c = 1 2 ( cos θ + i sin θ ) − 1 4 ( cos 2 θ + i sin 2 θ ) = 1 2 cos θ − 1 4 ( 2 cos 2 θ − 1 ) + i [ 1 2 sin θ − 1 4 2 cos θ sin θ ] = 1 4 + 1 2 ( 1 − cos θ ) cos θ + i 1 2 ( 1 − cos θ ) sin ( θ ) = 1 4 + 1 2 ( 1 − cos θ ) e i θ \begin{align*}
c &=\frac12(\cos\theta+i\sin\theta)-\frac14(\cos2\theta+i\sin 2\theta) \\
&=\frac12\cos\theta-\frac{1}{4}(2\cos^2\theta-1)+i\left[\frac12\sin\theta-\frac1{4}2\cos\theta\sin\theta\right]\\
&=\frac14+\frac12(1-\cos\theta)\cos\theta+i\frac12(1-\cos\theta)\sin(\theta)\\
&=\frac14+\frac12(1-\cos\theta)e^{i\theta}
\end{align*} c = 2 1 ( cos θ + i sin θ ) − 4 1 ( cos 2 θ + i sin 2 θ ) = 2 1 cos θ − 4 1 ( 2 cos 2 θ − 1 ) + i [ 2 1 sin θ − 4 1 2 cos θ sin θ ] = 4 1 + 2 1 ( 1 − cos θ ) cos θ + i 2 1 ( 1 − cos θ ) sin ( θ ) = 4 1 + 2 1 ( 1 − cos θ ) e i θ 即邊界為心臟線。
分析二次實函數 f c ( x ) = x 2 + c f_c(x)=x^2+c f c ( x ) = x 2 + c c ∈ R c\in\mathbb{R} c ∈ R [解] 由 f c ( x ) = x f_c(x)=x f c ( x ) = x x 2 − x + c = 0 x^2-x+c=0 x 2 − x + c = 0 x = 1 ± 1 − 4 c 2 x=\frac{1\pm\sqrt{1-4c}}{2} x = 2 1 ± 1 − 4 c f ′ ( c ) = 2 x f'(c)=2x f ′ ( c ) = 2 x
當 c < 1 4 c<\frac14 c < 4 1 1 − 4 c > 0 1-4c>0 1 − 4 c > 0 x = 1 2 ± 1 − 4 c 2 x=\frac12\pm\frac{\sqrt{1-4c}}{2} x = 2 1 ± 2 1 − 4 c f ′ ( 1 2 − 1 − 4 c 2 ) = 1 − 1 − 4 c < 1 f'(\frac12-\frac{\sqrt{1-4c}}{2})=1-\sqrt{1-4c}<1 f ′ ( 2 1 − 2 1 − 4 c ) = 1 − 1 − 4 c < 1 x = 1 2 − 1 − 4 c 2 x=\frac12-\frac{\sqrt{1-4c}}{2} x = 2 1 − 2 1 − 4 c f ′ ( 1 2 + 1 − 4 c 2 ) = 1 + 1 − 4 c > 1 f'(\frac12+\frac{\sqrt{1-4c}}{2})=1+\sqrt{1-4c}>1 f ′ ( 2 1 + 2 1 − 4 c ) = 1 + 1 − 4 c > 1 x = 1 2 + 1 − 4 c 2 x=\frac12+\frac{\sqrt{1-4c}}{2} x = 2 1 + 2 1 − 4 c 當 c = 1 4 c=\frac14 c = 4 1 x = 1 2 x=\frac12 x = 2 1 f ′ ( 1 2 ) = 1 f'(\frac12)=1 f ′ ( 2 1 ) = 1 當 c > 1 4 c>\frac14 c > 4 1 x = 1 ± 1 − 4 c 2 ∈ C x=\frac{1\pm\sqrt{1-4c}}{2}\in\mathbb{C} x = 2 1 ± 1 − 4 c ∈ C 針對函數 L r ( x ) = r x ( 1 − x ) L_r (x)= r x (1-x) L r ( x ) = r x ( 1 − x ) f c ( x ) = x 2 + c f_c (x)=x^2+c f c ( x ) = x 2 + c 考慮兩個實數定點迭代式 x n + 1 = L r ( x n ) , r ∈ [ 0 , 4 ] x_{n+1}=L_r (x_n ), ~ r\in[0,4] x n + 1 = L r ( x n ) , r ∈ [ 0 , 4 ] x n + 1 = f c ( x n ) , c ∈ [ − 2 , 1 4 ] x_{n+1}=f_c (x_n),~c\in[-2,\frac14] x n + 1 = f c ( x n ) , c ∈ [ − 2 , 4 1 ] O ( x 0 ; L r ) \mathcal{O}(x_0;L_r) O ( x 0 ; L r ) O ( 0 ; f c ) \mathcal{O}(0;f_c ) O ( 0 ; f c ) x 0 ≠ 0 x_0\neq 0 x 0 = 0 請嘗試找出將 L r ( ξ ) L_r(\xi) L r ( ξ ) f c ( x ) f_c(x) f c ( x ) r ∈ [ 0 , 4 ] r\in[0,4] r ∈ [ 0 , 4 ] c ∈ [ − 2 , 1 4 ] c\in[-2,\frac14] c ∈ [ − 2 , 4 1 ] [解] Claim: 變換式為: x n = r ( 1 2 − ξ n r ) , c = r 2 ( 1 − r 2 ) x_n = r\left(\frac12-\frac{\xi_n}{r}\right),~c=\frac{r}{2}\left(1-\frac{r}{2}\right) x n = r ( 2 1 − r ξ n ) , c = 2 r ( 1 − 2 r )
由 ξ n + 1 = L r ( ξ n ) = r ξ n ( 1 − ξ n ) \xi_{n+1}=L_r(\xi_n) = r \xi_n (1-\xi_n) ξ n + 1 = L r ( ξ n ) = r ξ n ( 1 − ξ n )
x n + 1 = x n 2 + c ⟹ r ( 1 2 − ξ n + 1 r ) = r 2 ( 1 2 − ξ n r ) 2 + r 2 ( 1 − r 2 ) = r 2 4 − r ξ n + ξ n 2 + r 2 − r 2 4 ⟹ r 2 − ξ n + 1 = r 2 + ξ n 2 − r ξ n ⟹ ξ n + 1 = r ξ n − ξ n 2 = r ξ n ( 1 − ξ n ) \begin{align*}
&\quad x_{n+1} = x_n^2+c \\
\implies & r \left(\frac12 - \frac{\xi_{n+1}}{r}\right) =
r^2\left(\frac12 - \frac{\xi_n}{r}\right)^2+\frac{r}{2}\left(1-\frac{r}{2}\right)=\frac{r^2}4-r \xi_n+\xi_n^2+\frac{r}{2}-\frac{r^2}{4} \\
\implies & \frac{r}2 - \xi_{n+1} =
\frac{r}{2}+\xi_n^2-r\xi_n \\
\implies & \xi_{n+1}=r\xi_n-\xi_n^2=r \xi_n \left(1-\xi_n\right)
\end{align*} ⟹ ⟹ ⟹ x n + 1 = x n 2 + c r ( 2 1 − r ξ n + 1 ) = r 2 ( 2 1 − r ξ n ) 2 + 2 r ( 1 − 2 r ) = 4 r 2 − r ξ n + ξ n 2 + 2 r − 4 r 2 2 r − ξ n + 1 = 2 r + ξ n 2 − r ξ n ξ n + 1 = r ξ n − ξ n 2 = r ξ n ( 1 − ξ n ) 由 c = g ( r ) = r 2 ( 1 − r 2 ) = 1 4 − ( 1 4 − r 2 + r 2 4 ) = 1 4 − 1 4 ( 1 − r ) 2 c=g(r)=\frac{r}{2}\left(1-\frac{r}{2}\right)=\frac14-(\frac14-\frac{r}{2}+\frac{r^2}{4})=\frac14-\frac14(1-r)^2 c = g ( r ) = 2 r ( 1 − 2 r ) = 4 1 − ( 4 1 − 2 r + 4 r 2 ) = 4 1 − 4 1 ( 1 − r ) 2 r ∈ [ 0 , 4 ] r\in[0,4] r ∈ [ 0 , 4 ] g g g 1 4 \frac14 4 1 r = 1 r=1 r = 1 min { g ( 0 ) , g ( 4 ) } = − 2 \min\{g(0),g(4)\}=-2 min { g ( 0 ) , g ( 4 )} = − 2 r ∈ [ 0 , 4 ] r\in[0,4] r ∈ [ 0 , 4 ] c ∈ [ − 2 , 1 4 ] c\in[-2,\frac14] c ∈ [ − 2 , 4 1 ]
假設 { z 0 , z 1 } \{z_0,z_1\} { z 0 , z 1 } F F F g 2 ( z ) = F ( F ( z ) ) g_2(z)=F(F(z)) g 2 ( z ) = F ( F ( z )) g 2 ′ ( z 0 ) = g 2 ′ ( z 1 ) g_2'(z_0)=g_2'(z_1) g 2 ′ ( z 0 ) = g 2 ′ ( z 1 ) [解] 設 { z 0 , z 1 } \{z_0,z_1\} { z 0 , z 1 } F F F g 2 ( z 0 ) = z 1 g_2(z_0)=z_1 g 2 ( z 0 ) = z 1 g 2 ( z 1 ) = z 0 g_2(z_1)=z_0 g 2 ( z 1 ) = z 0 g 2 ′ ( z ) = F ′ ( F ( z ) ) F ′ ( z ) g_2'(z)=F'(F(z))F'(z) g 2 ′ ( z ) = F ′ ( F ( z )) F ′ ( z )
g 2 ( z 0 ) = F ′ ( F ( z 0 ) ) F " ( z 0 ) = F ′ ( z 1 ) F ′ ( z ) ) , g 2 ( z 1 ) = F ′ ( F ( z 1 ) ) F " ( z 1 ) = F ′ ( z ) F ′ ( z ) ) , g_2(z_0)=F'(F(z_0))F"(z_0)=F'(z_1)F'(z_)), \\
g_2(z_1)=F'(F(z_1))F"(z_1)=F'(z_)F'(z_)), g 2 ( z 0 ) = F ′ ( F ( z 0 )) F " ( z 0 ) = F ′ ( z 1 ) F ′ ( z ) ) , g 2 ( z 1 ) = F ′ ( F ( z 1 )) F " ( z 1 ) = F ′ ( z ) F ′ ( z ) ) , 故 g 2 ′ ( z 0 ) = g 2 ′ ( z 1 ) g_2'(z_0)=g_2'(z_1) g 2 ′ ( z 0 ) = g 2 ′ ( z 1 )