4.3 幾何級數與收歛定理 (Geometric Series and Convergence Theorems)

範例4.3-1. 討論 $\sum\limits_{n=0}^\infty z^n$ 的收歛情形。

• [解]

  1. 當 $|z|\ge 1$ 時，因 $\lim\limits_{n\to \infty} |z|^n=1$ 或 $\infty$，即 $\lim\limits_{n\to \infty} |z|^n \neq 0$，故 $\sum\limits_{n=0}^\infty z^n$ 發散。
     1. 當 $|z|< 1$ 時，因 $\lim\limits_{n\to \infty} |z|^n=0$，即 $\lim\limits_{n\to \infty} z^n =0$，以及

        $$\sum_{n=0}^N z^n =1 +z +z^2+\cdots+z^N=\frac{1-z^{N+1}}{1-z},$$

        因此

        $$\sum_{n=0}^\infty z^n = \lim_{N\to \infty} \sum_{n=0}^N = \lim_{N\to \infty}\frac{1-z^{N+1}}{1-z} =\frac{1}{1-z}.$$

  由上述兩點，歸納得

  $$\sum_{n=0}^\infty z^n =\begin{cases} \displaystyle\frac{1}{1-z}, & |z|<1 \\ \\ \text{發散},& |z|\ge 1. \end{cases}$$

由此例可以推得下列結論成立：

範例4.3-2. 設 $|r|<1$，求 $\sum\limits_{n=0}^\infty r^n \cos n\theta$ 以及 $\sum\limits_{n=0}^\infty r^n \sin n\theta$ 的收歛值。

• [解]

  令 $z=r e^{i\theta}=r\cos\theta+i r \sin\theta$，則 $z^n = r^n \cos n\theta+i r^n \sin n\theta$，由例題4.3-1知

  $$\begin{align*} \sum_{n=0}^\infty (r^n \cos n\theta +i r^n \sin n\theta) &= \sum_{n=0}^\infty z^n = \frac1{1-z}\quad (\because |z|=r<1) \\ &=\frac1{1-r\cos \theta -i r \sin\theta} = \frac{1-r\cos \theta +i r \sin\theta}{(1-r\cos\theta)^2+r^2\sin^\theta}\\ &= \frac{1-r\cos \theta }{1+r^2-2 r\cos\theta} + i\frac{r \sin\theta}{1+r^2-2 r\cos\theta} \end{align*}$$

  所以

  $$\sum_{n=0}^\infty r^n \cos n\theta =\frac{1-r\cos\theta}{1+r^2-2r\cos\theta},\quad \sum_{n=0}^\infty r^n \sin n\theta =\frac{r\sin\theta}{1+r^2-2r\cos\theta}.$$

範例4.3-3. 推導 $\displaystyle\sum_{n=0}^\infty \frac{(1-i)^n}{2^n}=1-i$ 。

• [解]

  因 $\displaystyle\sum_{n=0}^\infty \frac{(1-i)^n}{2^n}=\sum_{n=0}^\infty \left(\frac{1-i}{2}\right)^n$，令 $\displaystyle z=\frac{1-i}{2}$，則有 $\displaystyle |z|=\left|\frac{1-i}{2}\right|=\frac{1}{\sqrt{2}}<1$， 由例題4.3-1知

  $$\sum_{n=0}^\infty \frac{(1-i)^n}{2^n}=\frac{1}{1-\frac{1-i}{2}} =\frac{2}{2-(1-i)}=\frac{2(1-i)}{2}=1-i.$$

範例4.3-4. 計算 $\displaystyle\sum_{n=3}^\infty \left(\frac{i}{2}\right)^n$之值 。

• [解]

  $$\begin{align*} \sum_{n=3}^\infty \left(\frac{i}{2}\right)^n&=\sum_{n=0}^\infty \left(\frac{i}{2}\right)^n - \left[\left(\frac{i}{2}\right)^0+\left(\frac{i}{2}\right)^1+\left(\frac{i}{2}\right)^2\right] \\ &=\frac{1}{1-\frac{i}{2}}-\left[1+\frac{i}{2}-\frac{1}{4}\right]\quad(\because \left|\frac{i}{2}\right|=\frac12<1)\\ &=\frac{2}{2-i}-\frac{3+2i}{4}=\frac{2(2+i)}{5}-\frac{3+2i}{4}\\ &=\frac{1-2i}{20} \end{align*}$$

定理4.3-1. (比值測試)
給定
$\sum\limits_{n=0}^\infty z^n$，其中 $\displaystyle\lim_{n\to \infty} \left| \frac{z_{n+1}}{z_n}\right|=L$，則有

1. 若 $L<1$，則 $\sum\limits_{n=0}^\infty z^n$ 收斂。

2. 若 $L>1$，則 $\sum\limits_{n=0}^\infty z^n$ 發散。

3. 若 $L=1$，則 無法判定 $\sum\limits_{n=0}^\infty z^n$ 之斂散性。

• [證明]

  已知 $\displaystyle\lim_{n\to \infty} \left| \frac{z_{n+1}}{z_n}\right|=L$ 即

  $$\begin{align*} \forall \varepsilon>0,~\exists N_\varepsilon \text{~s.t.~} \forall n\ge N_\varepsilon &\implies \left| \left| \frac{z_{n+1}}{z_n}\right|-L\right|<\varepsilon\\ &\implies \left| \frac{z_{n+1}}{z_n}\right|<L+\varepsilon\implies |z_{n+1}|<(L+\varepsilon)|z_n| \end{align*}$$

  因此當 $L<1$， $\exists \varepsilon_0>0 \text{~s.t.~}L+\varepsilon_0<1$。對這個 $\varepsilon_0$，從上面關係式可知

  $$\exists N_{\varepsilon_0} \text{~s.t.~} \forall n\ge N_{\varepsilon_0}\implies |z_{n+1}|<r |z_n|,\quad r=L+\varepsilon_0<1,$$

  因此

  $$\sum_{m=1}^{\infty} \left| z_{N_{\varepsilon_0}+m} \right| <\sum_{m=1}^{\infty} r^m \left| z_{N_{\varepsilon_0}} \right| = \left| z_{N_{\varepsilon_0}} \right| \sum_{m=1}^{\infty} r^m=\frac{\left| z_{N_{\varepsilon_0}} \right|}{1-r}\quad(\because r<1)$$

  即 $\sum\limits_{m=1}^{\infty} \left| z_{N_{\varepsilon_0}+m} \right|$ 收斂，因此

  $$|z_0|+|z_1|+\cdots+|z_{N_{\varepsilon_0}}|+\sum_{m=1}^{\infty} \left| z_{N_{\varepsilon_0}+m} \right|=\sum_{n=0}^{\infty} \left| z_{n} \right|$$

  收斂，得證。

  其他兩個情形的證明，自行練習。$\hspace{6cm}\blacksquare$

範例4.3-5. 說明 $\displaystyle\sum_{n=0}^\infty \frac{(1-i)^n}{n!}$收斂 。

• [解]

  因 $\displaystyle\lim_{n\to \infty} \left| \frac{\frac{(1-i)^{n+1}}{(n+1)!}}{\frac{(1-i)^n}{n!}} \right|=\lim_{n\to \infty} \left| \frac{1-i}{n+1} \right|=0<1$，由比值測試知級數 $\displaystyle\sum_{n=0}^\infty \frac{(1-i)^n}{n!}$收斂。

定義4.3-1. ( Limit Supremum)

給定 $\{t_n\}\subset \mathbb{R}$，$\limsup\limits_{n\to\infty} t_n=L$ 之充要條件為最小實數 $L$ 使得 $\forall \varepsilon>0$，存在最多有限項的 $t_n>L+\varepsilon$。反之，若這種 $L$ 不存在，則記為 $\limsup\limits_{n\to\infty} t_n=\infty$ 。

由此定義，明顯地 $\limsup\limits_{n\to\infty} t_n=L$ 同義於

定義圖示如下：

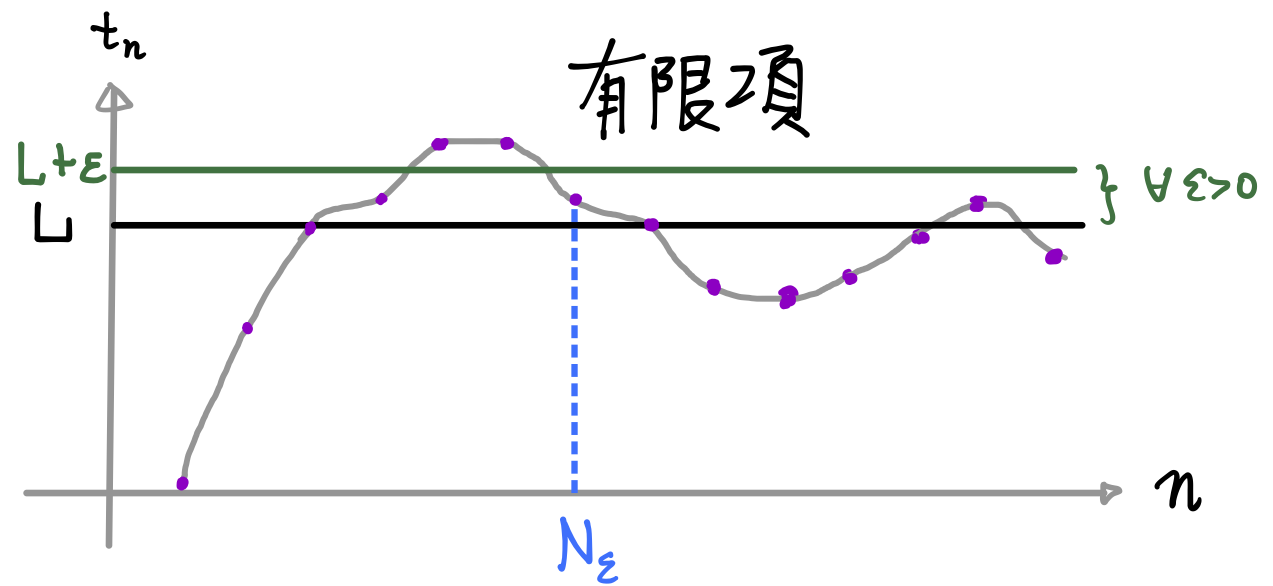
範例4.3-6.

1. $\{t_n\}=\{1,2,3,1,2,3\ldots\}$， $\limsup\limits_{n\to \infty} t_n=3$。

2. $\{a_n\}=\{4,5,4.01,5.01,4.001,5.001\ldots\}$， $\limsup\limits_{n\to \infty} a_n=5$。

3. $\{b_n\}=\{1+\frac1n\}$， $\limsup\limits_{b\to \infty} b_n=1$；注意因 $\lim\limits_{n\to\infty} b_n=1$(極限存在，如此 $\limsup\limits_{n\to\infty}b_n=\lim\limits_{n\to\infty}b_n$)。

4. $\{f_n\}=\{1,1,2,3,5,8,13,21,\ldots\}$， $\limsup\limits_{n\to \infty} f_n=\infty$。

定理4.3-2. (根號測試)
給定
$\sum\limits_{n=0}^\infty z^n$，其中 $\displaystyle\limsup_{n\to \infty} \left| z_n\right|^{\frac1n}=L$，則有

1. 若 $L<1$，則 $\sum\limits_{n=0}^\infty z^n$ 收斂。

2. 若 $L>1$，則 $\sum\limits_{n=0}^\infty z^n$ 發散。

3. 若 $L=1$，則 無法判定 $\sum\limits_{n=0}^\infty z^n$ 之斂散性。

• [證明]

  已知 $\displaystyle\limsup_{n\to \infty} \left| z_n\right|^{\frac1n}=L$ 即

  $$\begin{align*} \forall \varepsilon>0,~\exists N_\varepsilon \text{~s.t.~} \forall n\ge N_\varepsilon &\implies \left| z_n\right|^\frac1n<L+\varepsilon\triangleq r \implies |z_n|<r^n\\ &\implies \sum_{n=N_\varepsilon}^\infty |z_n|<\sum_{n=N_\varepsilon}^\infty r^n \end{align*}$$

  因此當 $L<1$， $\exists \varepsilon_0>0 \text{~s.t.~}L+\varepsilon_0<1$。對這個 $\varepsilon_0$，有一個 $N_{\varepsilon_0}$ 使得 $\sum_{n=N_\varepsilon}^\infty r^n$ 收斂， $\sum\limits_{n=N_\varepsilon}^\infty |z_n|$ 收斂，再加入 $z_0,~z_1,\ldots,z_{N_{\varepsilon_0}-1}$，則 $\sum\limits_{n=0}^\infty |z_n|$ 收斂，得證。
  其他兩個情形的證明，自行練習。
  $\hspace{6cm}\blacksquare$

範例4.3-7. 決定 $\displaystyle\sum_{n=0}^\infty z_n = 3 +4^2+3^3+4^4+3^5+4^6+\cdots$是否收斂？

• [解]

  因 $\{|z_n|^\frac1n\}=\{3,4,3,4,3,4,\ldots\}$，故 $\limsup\limits_{n\to \infty} |z_n|^\frac1n=4>1$，由根號測試知級數 $\displaystyle\sum_{n=0}^\infty z_n$ 發散。