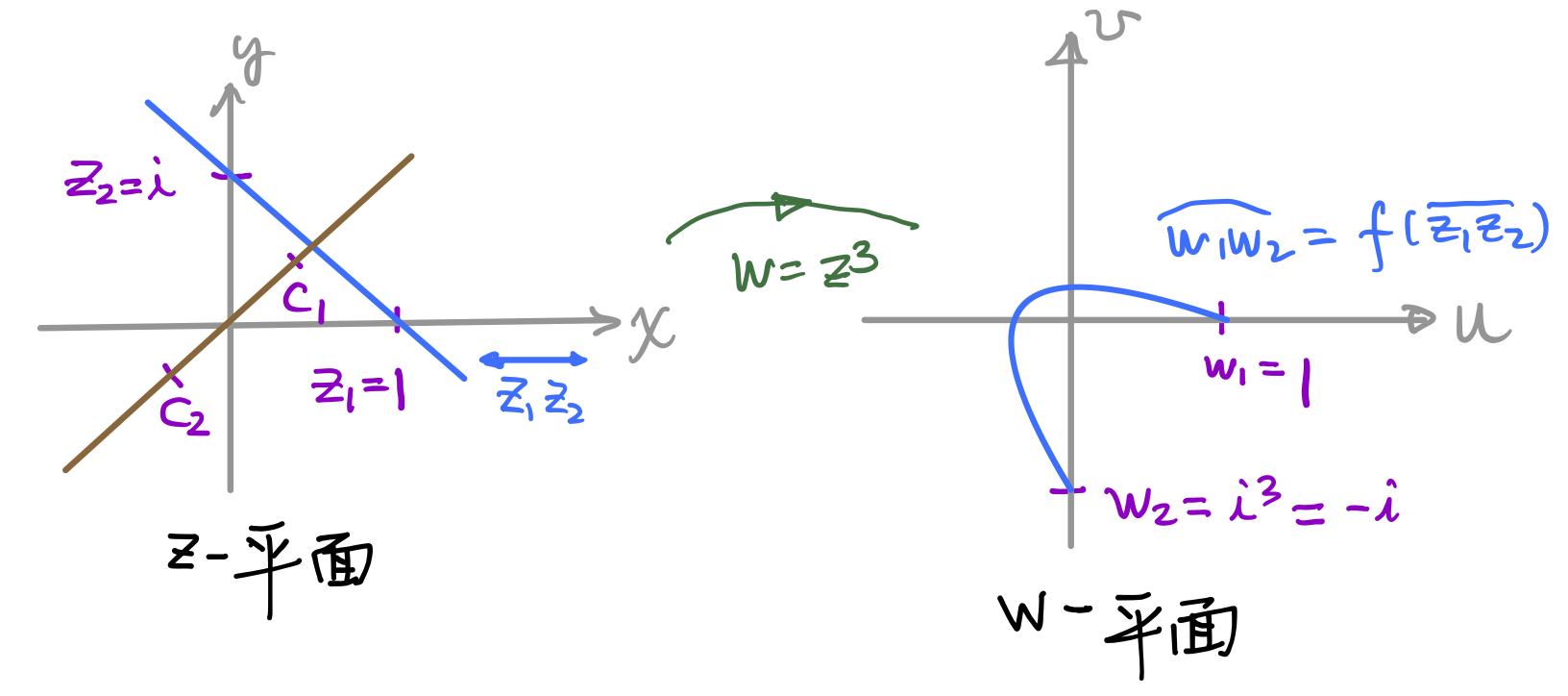3.1 可微與解析函數 (Differentiable and Analytic Functions)

可微分性

定義3.1-1. 設 $f$ 定義在 $z_0$ 之某一個鄰域。若極限

\begin{equation*} \lim_{z\to z_0}\frac{f(z)-f(z_0)}{z-z_0}=\lim_{\Delta z\to 0}\frac{f(z_0+\Delta z)-f(z_0)}{\Delta z} \end{equation*}

存在，則稱 $f$ 在點 $z_0$ 是可微分的(differentiable)，這個極限值稱為 $f$ 在 $z_0$ 之導數(derivative)，記作 $f'(z_0)$ 或 $\frac{df}{dz}(z_0)=\frac{df}{dz}\Big|_{z_0}$ ，即

\begin{equation} f'(z_0)=\lim_{z\to z_0}\frac{f(z)-f(z_0)}{z-z_0}=\lim_{\Delta z\to 0}\frac{f(z_0+\Delta z)-f(z_0)}{\Delta z} \tag{3.1-1} \end{equation}

上述定義中，若令 $\Delta f(z_0)=f(z_0+\Delta z)-f(z_0)$ ，則可得到Leibniz的表示式，即導數是瞬間變化率：

f'(z_0)=\lim_{\Delta z\to 0}\frac{\Delta f(z_0)}{\Delta z}

在複變函數的討論，不再如微積分討論單變數函數微分時，用切線斜率來說明函數的導數，因為已經很難從圖形上來描述或呈現所謂的「切線斜率」的概念，但瞬間變化率仍是一個適切的角度來理解導數。

再令 $\varepsilon(\Delta z)=\Delta f-f'(z_0)\Delta z$ ，由 $(3.1\text{-}1)$ 式知

\lim_{\Delta z\to 0} \frac{f'(z_0+\Delta z)-f(z_0)-f'(z_0)\Delta z}{\Delta z}=0\implies \lim_{\Delta z\to 0}\frac{\varepsilon(\Delta z)}{\Delta z}=0,

故當 $f$ 在 $z_0$ 可微則在 $z_0$ 之鄰域上，下列關係成立：

\begin{equation} f(z_0+\Delta z)=f(z_0)+f'(z_0)\Delta z+\varepsilon(\Delta z) \tag{3.1-2} \end{equation}

即是所謂的線性近似 (linearization)

\begin{equation} \Delta f(z_0)=f'(z_0)\Delta z+\varepsilon(\Delta z) \tag{3.1-3} \end{equation}

設 $f'(z)=\rho e^{i \phi}$ ，表示 $w$ -平面的變化量 $\Delta f$ 的變化，相當於將 $z$ -平面的變化量，乘以 $\rho$ 倍再旋轉 $\phi$ 的角度。

當 $\Delta z\to 0$ 時，由 $(3.1\text{-}2)$ 得

\lim_{\Delta z\to 0}\Delta f(z_0)=\lim_{\Delta z\to 0}f(z_0+\Delta z)-f(z_0)=\lim_{\Delta z\to 0}f'(z_0)\Delta z+\varepsilon(\Delta z)= f'(z_0) dz

$f'(z_0) dz$ 稱為 $f$ 在 $z_0$ 之微分量(differential)，以 $df(z_0)$ 表之。

例題3.1-1. 當 $f(z)=z^3$ 時，計算 $f'(3)$ 與 $f'(z)$ 。

[解]
$f'(3) =\lim_{z\to 3}\frac{f(z)-f(3)}{z-3} =\lim_{z\to 3}\frac{z^3-3^3}{z-3} =\lim_{z\to 3}z^2+3z+9=3^2+3\cdot 3+9=27.$
又
$f'(z) =\lim_{\Delta z\to 0}\frac{f(z+\Delta z)-f(z)}{\Delta z} =\lim_{\Delta z\to 0}\frac{(z+\Delta z)^3-z^3}{\Delta z} =\lim_{\Delta z\to 0}3z^2+3 z(\Delta z)+(\Delta z)^2=3 z^2.$
當然可以先算 $f'(z)$ ，在算 $f'(3)=f'(z)\big|_{z=3}$ ，結果相同。目前作法，展示了兩種計算導數的方式。

例題3.1-2. 討論 $f(z)=\text{Re}~z$ 的可微分性。

[解]
設 $z=x+iy, z_0=x_0+iy_0$ ，
$\displaystyle \lim_{z\to z_0}\frac{f(z)-f(z_0)}{z-z_0}=\lim_{z\to z_0}\frac{\text{Re}(z-z_0)}{z-z_0} \begin{cases} {=\atop{\small \text{沿}y=y_0}} \lim_{x\to x_0}\frac{x-x_0}{x-x_0}=\lim_{x\to x_0}1=1, \\ \\ {=\atop{\small \text{沿}x=x_0}} \lim_{y\to y_0}\frac{0}{i(y-y_0)}=\lim_{x\to x_0}0=0\end{cases}$
上面兩個方向之極限並相同，因此上述極限不存在，即函數不可微。然而此函數在任意點均連續，因此 $f(z)=\text{Re~}z$ 在複數平面上處處連續但不可微。

例題3.1-3. 討論 $f(z)=\bar{z}$ 的可微分性。

[解]
設 $z=x+iy, z_0=x_0+iy_0$ ，則 $\bar{z}=x-iy,~\bar{z}_0=x_0-i y_0$ ，因此
$\displaystyle \lim_{z\to z_0}\frac{f(z)-f(z_0)}{z-z_0}=\lim_{z\to z_0}\frac{\bar{z}-\bar{z}_0}{z-z_0} \begin{cases} {=\atop{\small \text{沿}y=y_0}} \lim_{x\to x_0}\frac{x-x_0}{x-x_0}=\lim_{x\to x_0}1=1, \\ \\ {=\atop{\small \text{沿}x=x_0}} \lim_{y\to y_0}\frac{-i(y-y_0)}{i(y-y_0)}=\lim_{x\to x_0}-1=-1\end{cases}$
上面兩個方向之極限並不相同，因此上述極限不存在，即函數不可微。然而此函數在任意點均連續，因此 $f(z)=\bar{z}$ 在複數平面上處處連續但不可微。

微分規則： 設 $n\in\mathbb{C}, c\in\mathbb{C}$ ，

1. $\frac{d}{dz}c=0$ ,	7. $\frac{d}{dz}z^{n}= n z^{n-1}$
3. $\frac{d}{dz}\big[f(z)\pm g(z)\big]=\frac{d f}{dz} \pm \frac{d g}{dz} = f'(z)\pm g'(z)$	4. $\frac{d}{dz}\big[c f(z)\big]=c \frac{d f}{dz}=c f'(z)$
5. $\frac{d}{dz}\big[f(z)\cdot g(z)\big]=\frac{d f}{dz} g(z)+f(z) \frac{d g}{dz}$	6. $\frac{d}{dz}\left[\frac{f(z)} {g(z)}\right]=\frac{f'(z)g(z)-f(z)g'(z)}{g(z)^2}$
7. $\frac{d}{dz}z^{-n}= (-n) z^{-n-1}=-n z^{-(n+1)}$	8. $\frac{d}{dz}\big[f(z)\big]^n =n \big[f(z)\big]^{n-1} f'(z)$

[證明] 自行利用微分定義練習。

定理3.1-1. 若函數 $f$ 在 $z_0$ 可微，則f 在 $z_0$ 連續。

[證明] 與單變數實數函數的證法一樣，自行練習。

對多項式 $p(z)=a_n z^n+a_{n-1} z^{n-1}+\cdots+a_2 z^2+a_1 z+a_0$ 而言，其導數為 $p'(z)=n a_n z^{n-1}+(n-1) a_{n-1} z^{n-2}+\cdots+2 a_2 z+ a_1$ 。

解析性

函數的解析性討論的是函數不只在該點可微，連這點的鄰域上的點都可微，亦即在該點附近函數是平滑的，表示該函數在此點附近的變化可以用多項式或是冪級數來近似。解析性的正式定義如下。

定義3.1-2. 設 $z_0 \in \mathbb{C}$ 。若存在 $\delta>0$ 使得函數 $f$ 在 $z_0$ 的鄰域 $D_\delta(z_0)$ 內的任意點均可微分，則 $f$ 在 $z_0$ 點解析(analytic)、全純(holomorphic)或正則 (regular) 表示。反之， $f$ 的非解析 (non-analytic) 的點，稱為 $f$ 的奇異點 (singular point)。

這一個觀念和在 $z_0$ 可微分是不一樣的，當然若 $f$ 在 $z_0$ 點解析則 $f$ 在 $z_0$ 點可微分，但反若 $f$ 在 $z_0$ 點不可微則 $f$ 在 $z_0$ 點非解析。

定義3.1-2. 若 $f$ 在域 $\mathcal{D}$ 內之每一個點均可微，則 $f$ 在 $\mathcal{D}$ 均可微分，並 $f$ 在 $\mathcal{D}$ 均可解析。若 $\mathcal{D}$ 為整個複數平面 $\Complex$ ，則此解析函數稱為整函數 (entire function) 或全純函數 (holomorphic function)。

為何當 $f$ 在 $\mathcal{D}$ 均可微分，並 $f$ 在 $\mathcal{D}$ 均可解析，此因 $\mathcal{D}$ 內任意點的鄰域也在 $\mathcal{D}$ 內，均是可微。所有在域 $\mathcal{D}$ 上解析函數函數所成的集合表為 $\mathscr{A}(\mathcal{D})$ ：

\mathscr{A}(D)=\{f:\mathcal{D}\subseteq\mathbb{C}\to \mathbb{C}~|~f \text{為解析}\}.

與實數分析一樣，解析的運算法則仍然成立。可微、解析與全純函數集合間之類別關係如下：

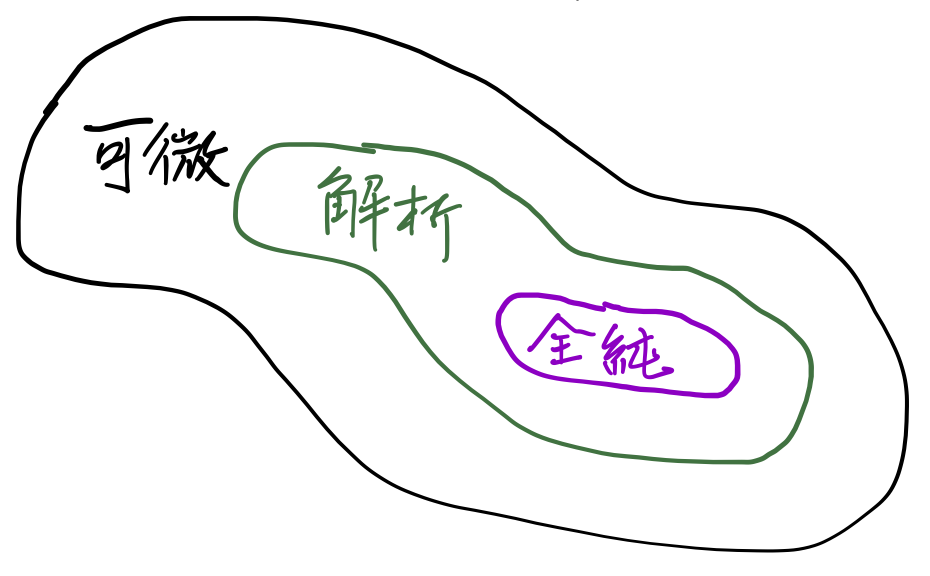
圖3.1-1 可微函數間之類別關係

定理3.1-2. 若函數 $f,g$ 在域 $\mathcal{D}$ 內解析則 $f\pm g,~f\cdot g$ 在 $\mathcal{D}$ 內亦解析，

\begin{align*} (f(z)\pm g(z))'&=f'(z)\pm g'(z) \\ (f(z)~g(z))'&=f'(z)g(z)+f(z)g'(z) \end{align*}

若 $\forall z \in \mathcal{D},~g(z)\ne 0$ ，則 $\frac{f}{g}$ 在 $\mathcal{D}$ 內解析，且

\left(\frac {f(z)}{g(z)}\right)'=\frac{f'(z)g(z)-f(z)g'(z)}{g^2(z)}

定理3.1-2. 若函數 $f$ 在域 $\mathcal{D}$ 在域 $E$ 解析且 $f(\mathcal{D}) \subset E$ 在域 $\mathcal{D}$ 亦解析，且 $(g(f(z)))=g(f(z))f'(z)$

[證]
與實數證明一樣，略。

例題3.1-4. 說明函數 $f(z)=|z|^2$ 在 $z=0$ 可微，但非解析。

[解]
由定義
$f'(0)=\lim_{z\to 0} \frac{|z|^2-0}{z-0} =\lim_{z\to 0} \frac{|z|^2}{z} =\lim_{z\to 0} \frac{z\bar{z}}{z} = \lim_{z\to 0} \bar{z} =0,$
因此此函數在 $z=0$ 可微。令 $z=r e^{i\theta},~z_0=r_0 e^{i\theta_0}~(r_0\neq 0)$ ，則
$\begin{align*} f'(z_0) &=\lim_{z\to z_0}\frac{|z|^2-|z_0|^2}{z-z_0} =\lim_{(r,\theta)\to (r_0,\theta_0)}\frac{r^2-r_0^2}{re^{i\theta}-r_0 e^{i\theta_0}}\\ &\begin{cases} {=\atop{\small \text{沿}\theta=\theta_0}} \lim\limits_{r\to r_0}\frac{r^2-r_0^2}{(r-r_0)e^{i\theta_0}} =\lim\limits_{r\to r_0}(r+r_0)e^{-i\theta_0}=2r_0e^{-i\theta_0}, \\ \\ {=\atop{\small \text{沿}r=r_0}} \lim\limits_{\theta\to \theta_0}\frac{0}{r_0(e^{i\theta}-e^{i\theta_0})}=0. \end{cases} \end{align*}$
即除 $z=0$ 外的任何點， $f(z)=|z|^2$ 均不可微；換句話說對任何 $z=0$ 的去心鄰域， $f$ 不可微，因此 $f(z)=|z|^2$ 在 $z=0$ 非解析。

羅必達規則

與微分有關的極限規則，先說明如下：

定理3.1-3. (羅必達規則，l’Hopital’s Rule)

設函數 $f,~g$ 在 $z_0$ 點解析。若 $f(z_0)=g(z_0)$ ，但 $g'(z_0)\neq 0$ ，則

\lim_{z\to z_0} \frac{f(z)}{g(z)} = \lim_{z\to z_0} \frac{f'(z)}{g'(z)}

[證明]
留待第7章再證明。

均值定理？

討論至此，不禁會問：在微積分時所學的均值定理(Mean Value Theorem)，是否仍然成立？亦即若 $f$ 為可微函數，則是否存在 $c\in\overline{z_1z_2}$ 使得

f'(c)=\frac{f(z_2)-f(z_1)}{z_2-z_1}

成立？

例題3.1-5. 設 $f(z)=z^3,~ z_1=i,~z_2=i$ ，說明均值定理不成立。

[解]
$f'(z)=3z^2$ ，由
$\frac{f(z_2)-f(z_1)}{z_2-z_1} = \frac{i^3-1^3}{i-1}=i^2+i+1=i\triangleq f'(c)=3c^2$
解之得 $c_{1,2}=\pm \frac{1}{\sqrt{3}}e^{i\frac{\pi}{4}}$ 。但 $\overline{z_1z_2}=(1-t)z_1+tz_2=1+t(i-1),~t\in[0,1]$ ，從下圖
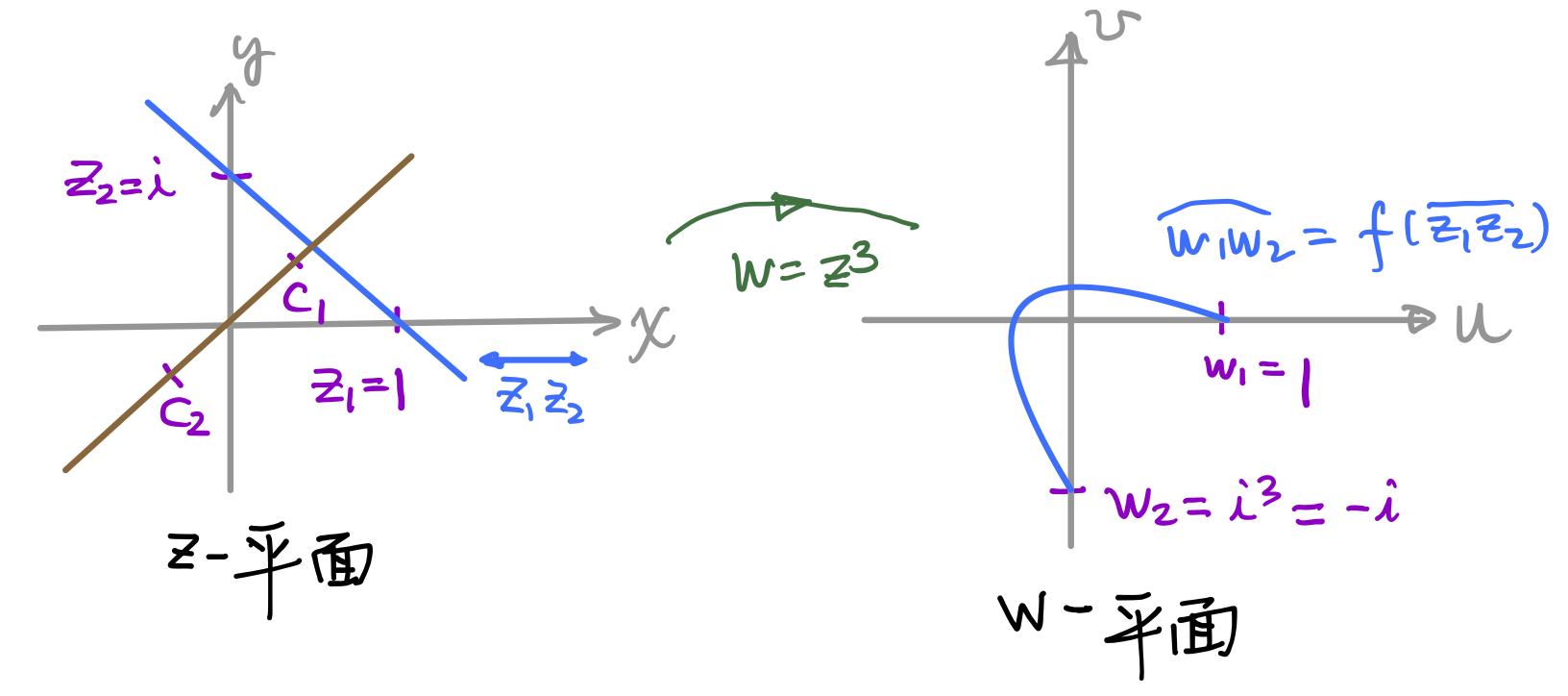
知 $c_1,~c_2\not\in \overline{z_1z_2}$ ，即均值定理不成立。