1.3 複數的幾何表示 (Geometric Representation of Complex Numbers)

複數的極座標

型如z=a+biz =a + biz=a+biz =a + bi aa、bb為實數，稱之為複數，其中i2=−1i^2=-1；aa 與 bb 分別稱為 zz 之實部 (real part) 與虛部 (image part) ，也記作 Re zz 和 Im zz 所有的複數所成之集合—複數系，以 C\Complex 表之。

任意的複數，均可以用平面上的有序對來表示，即在平面上，我們採用座標點 (a,b)(a,b) 表示複數 z=a+biz=a+bi；即實部與 xx 軸上的點對應，因此 xx 軸稱為實軸 (real axis) ；而虛部與 yy 軸上的點對應，yy 軸稱為虛軸 (image axis) 。此一由實軸與虛軸所展開之平面稱為複數平面 (complex plane) 或稱高斯平面 (Gauss plane)

(a,b)⟷a+bi(a,b) \longleftrightarrow a+bi

直角座標上之任一點與複數平面上之點有一個1−11-1對應關係，複數平面上之虛軸也經常以 iyiy 表示， 複數平面可圖示如下：

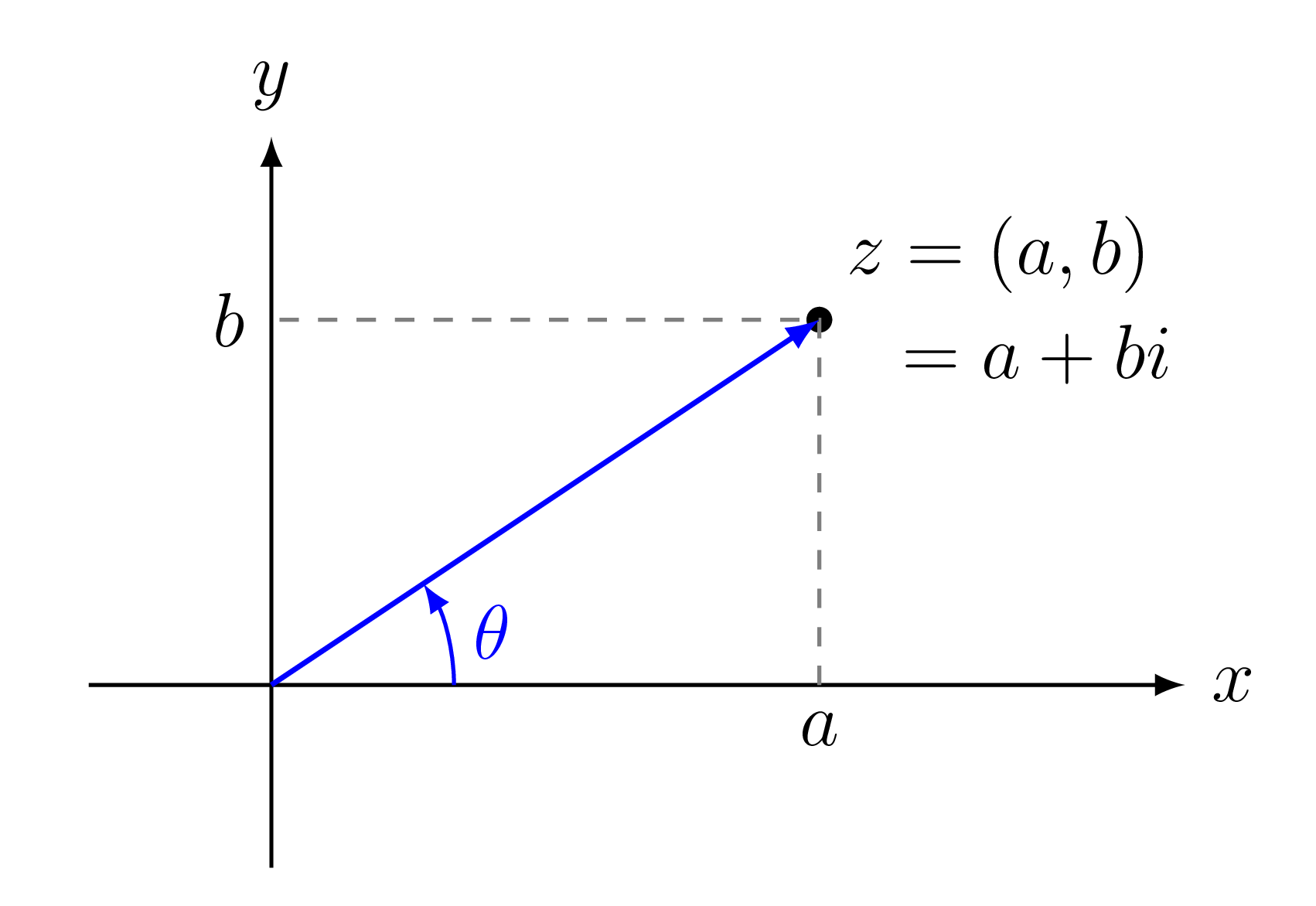
圖1.3-1: 複數平面 (Wessel-Argand plane)

Geogebra 1: 複數 zz 之極座標、長度與角度

https://www.geogebra.org/m/mm9bshum

z=a+biz=a+bi 可視為從 0 0 到 zz 之向量 oz→\overrightarrow {oz} ；oz→\overrightarrow {oz} 之長度即 zz 為之長度，記作 ∣z∣ \left| z \right| ，顯然

∣z∣=r=a2+b2\begin{equation} \left|z\right|=r=\sqrt{a^2+b^2} \tag{1.3-1} \end{equation}

假如 zz 不是原點 (z≠0z\ne0)，則 oz→\overrightarrow {oz} 與 xx 軸正方向之夾角 θ\theta 為 zz 之幅角 (argument or phase) 記作 arg zz，其方向規定反時針方向為正，逆時針方向為負，很顯然一個複數有無限多個幅角；若 θ\theta θ\thetazz 之一個幅角，則

θ+2nπ,n∈Z\theta+2n\pi, n\in \Z

即為複數全部幅角，故

arg⁡z={θ+2nπ,n∈Z}.\begin{equation} \arg z=\{\theta+2n\pi, n\in\Z\}. \tag{1.3-2} \end{equation}

在複數的幅角之中，有一個幅角 θ0\theta_0 在 (−π,π](-\pi, \pi] 之間，此稱為zz之主幅角或幅角之主值(principle value of the argument)，記作 Arg z\text{Arg}~z

Arg z=θ∈(−π,π],θ∈arg z\begin{equation} \text{Arg}~z=\theta \in (-\pi,\pi], \quad \theta\in\text{arg}~z \tag{1.3-3} \end{equation}

其實在每隔 2π2\pi 的區間均只有一個幅角，所以有時為了方便起見亦可以 (τ,2π+τ](\tau, 2\pi+\tau] 取 τ\tau 之主幅角，這時記作 arg⁡τz\arg_\tau z

arg⁡τz=θ∈(τ,2π+τ],θ∈arg z\begin{equation} \arg_\tau z=\theta\in(\tau,2\pi+\tau], \quad \theta\in\text{arg}~z\tag{1.3-4} \end{equation}

一般而言，選擇 τ∈[−π,π]\tau\in [-\pi,\pi] 。不論 arg⁡z\arg z 之 2π−2\pi-區間 如何選擇，均滿足

arg⁡z={arg⁡τz+2nπ,n∈Z}=⋃τ∈[−π,π]{arg⁡τz}(1.3-5)\begin{aligned} \arg z&=\{\arg_\tau z +2n\pi, n\in\Z\} \\ &=\bigcup_{\tau\in [-\pi,\pi]}\{\arg_\tau z\} \tag{1.3-5} \end{aligned}

因此 Arg z=arg⁡−πz\text{Arg}~z=\arg_{-\pi} z。

Geogebra 2: 幅角 Arg z\text{Arg}~z 與  arg⁡z~\arg z 之關係

https://www.geogebra.org/m/huyjedfn

例題1.3-1. 已知z=1+iz=1+i，計算 arg⁡ z\arg~z 與 Arg z\text {Arg}~ z。

例題1.3-2. 設 y∈Ry\in\R，

  1. Arg(yi)={π2,y>0,−π2,y<0.\text {Arg} (yi) = \begin{cases} \frac{\pi}{2}, & y>0, \\ -\frac{\pi}{2},& y<0. \end{cases}
  1. Arg i=π2,\text{Arg}~ i =\frac{\pi}{2},
  1. Arg 1=0.\text{Arg}~1=0.

注意：z=0z=0 的幅角即 Arg(0)\text{Arg}(0) 是不定義的，即在複數平面上除原點外之複數均可定義其幅角。

例題1.3-3. 求arg⁡(1+3i)\arg(1+\sqrt3i)、Arg z(1+3i)\text {Arg}~ z(1+\sqrt3i)以及arg⁡3π4(1+3i)\arg_\frac{3\pi}{4} (1+\sqrt3i)。

由圖1.3-1複數 z=a+biz=a+bi 可以由 zz 的長度及幅角來表示，

z=a+bi=r(cos⁡θ+isin⁡θ)\begin{equation} z=a+bi=r(\cos\theta+i\sin\theta) \tag{1.3-6} \end{equation}

其中 ∣z∣=r\left| z \right| =r ，θ∈arg⁡z\theta \in \arg z ，(1.3-6)式式稱為複數 zz 的極式 (polar form) ，由泰勒展開式知

cos⁡θ=1−12!θ2+14!θ4−…\cos\theta =1-\frac{1}{2!} \theta^2+\frac{1}{4!}\theta^4-\ldots
sin⁡θ=1−13!θ3+15!θ5−…\sin\theta=1-\frac{1}{3!}\theta^3+\frac{1}{5!}\theta^5-\ldots

代入(1.3-6)式得

z=r(1+iθ+12!(iθ)2+13!(iθ)3+14!(iθ)4+15!(iθ)5+…)\begin{equation*} z=r\left(1+i\theta+\frac {1}{2!} (i\theta)^2 +\frac {1}{3!} (i\theta)^3 +\frac {1}{4!} (i\theta)^4 +\frac {1}{5!} (i\theta)^5 + \ldots\right) \end{equation*}

如果我們引進一個新的定義：

定義1.3-1. 若 θ∈R\theta \in \R，則 eiθe^{i\theta} 為一複數且定義如下

eiθ=∑n=0∞(iθ)nn!(1.3-7)e^{i\theta} = \sum_{n=0}^{\infty} \frac{(i\theta)^n}{n!} \tag{1.3-7}

複數的指數函數在第五章才會定義，此處直接從實函數 exe^x 的泰勒 (Taylor) 級數來定義。由此定義則有

eiθ=1+iθ+(iθ)22!+(iθ)33!+(iθ)44!+(iθ)55!+(iθ)66!+(iθ)77!+⋯=1+iθ−θ22!−iθ33!+θ44!+iθ55!−θ66!−iθ77!++−−⋯=(1−θ22!+θ44!−θ66!+−⋯ )+i(θ−θ33!+θ55!−iθ77!+−⋯ )=cos⁡θ+isin⁡θ\begin{align*} e^{i\theta} &= 1+i\theta+\frac{(i\theta)^2}{2!}+\frac{(i\theta)^3}{3!} +\frac{(i\theta)^4}{4!} +\frac{(i\theta)^5}{5!} +\frac{(i\theta)^6}{6!} +\frac{(i\theta)^7}{7!} + \cdots \\ &= 1+i\theta-\frac{\theta^2}{2!}-i\frac{\theta^3}{3!} +\frac{\theta^4}{4!} +i\frac{\theta^5}{5!} -\frac{\theta^6}{6!} -i\frac{\theta^7}{7!} ++--\cdots \\ &=\left(1-\frac{\theta^2}{2!} +\frac{\theta^4}{4!} -\frac{\theta^6}{6!}+-\cdots\right)+i\left(\theta-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-i\frac{\theta^7}{7!}+-\cdots\right) \\ &=\cos\theta +i\sin\theta \end{align*}

亦即下式稱為 Euler 公式 (Euler Formulas) 成立：

 eiθ=cos⁡θ+isin⁡θ \begin{equation} \fcolorbox{blue}{FFFF37}{ $e^{i\theta} = \cos\theta +i\sin\theta$ } \tag{1.3-8} \end{equation}

當 θ=π\theta=\pi 時， 式(1.3-8)變成所有數學定理中最有名的 Euler 恆等式( Euler identity)：

 eiπ+1=0 \colorbox{FFFF37}{\color{blue} $e^{i\pi}+1=0$ }

此式之所以出名是因式子內包含有兩個無理數 ee 與 π\pi ，同時將虛數 ii 以及三角函數在內。

根據這一個定義複數 zz 的極式(1.3-6)可表成更簡單的形式

z=r(cos⁡θ+isin⁡θ)=reiθ=∣z∣eiθ\begin{equation} \begin{aligned} z&=r(\cos\theta+i\sin\theta)\\ &=re^{i\theta} =\left|z\right| e^{i\theta} \end{aligned} \tag{1.3-9} \end{equation}

式(1.3-9) 稱為複數 zz 的 Euler 式或極表示法 (polar form)。由定義1.3-1我們得到下列幾個等式

cos⁡θ=Re eiθ=eiθ+e−iθ2,sin⁡θ=Im eiθ=eiθ−e−iθ2i\begin{equation} \cos\theta=\text{Re}~e^{i\theta}=\frac{e^{i\theta}+e^{-i\theta}}{2},\quad \sin\theta=\text{Im}~e^{i\theta}=\frac{e^{i\theta}-e^{-i\theta}}{2i} \tag{1.3-10a} \end{equation}
∣eiθ∣=1\begin{equation} |e^{i\theta}|=1\tag{1.3-10b} \end{equation}
eiθ1⋅eiθ2=ei(θ1+θ2)\begin{equation} e^{i\theta_1} \cdot e^{i\theta_2}= e^{i(\theta_1+\theta2)}\tag{1.3-11} \end{equation}
eiθ1eiθ2=ei(θ1−θ2)\begin{equation} \frac{e^{i\theta_1}}{e^{i\theta_2}}= e^{i(\theta_1-\theta2)}\tag{1.3-12} \end{equation}

式(1.3−11)(1.3-11)表示乘積的幅角等於幅角和，式(1.3−12)(1.3-12)表示相除的幅角等於幅角差，即下面定理成立：

定理1.3-1. 若 z1≠0,z2≠0∈Cz_1\neq0, z_2\neq0 \in \cnums，則

arg⁡(z1z2)=arg⁡(z1)+arg⁡(z2)arg⁡(z1z2)=arg⁡(z1)−arg⁡(z2)\begin{align} \arg(z_1z_2)=\arg(z_1)+\arg(z_2) \tag{1.3-13a} \\ \arg\left(\frac{z_1}{z_2}\right)=\arg(z_1)-\arg(z_2) \tag{1.3-13b} \end{align}

例題1.3-4. 求 (5−i)4(1+i)(5-i)^4(1+i)，並證明 π4=4tan⁡−115−tan⁡−11239\frac {\pi}{4} = 4\tan{}^{-1} \frac{1}{5}-\tan{}^{-1} \frac{1}{239}。

例題1.3-5. i−4321 i^{-4321} 之值為多少，可以先計算 i4320=i4⋅1080=(i4)1080=11080=1i^{4320}=i^{4\cdot 1080}= (i^4)^{1080} =1^{1080}=1，因此

i−4321=1i4321=1i⋅i4320=1i=i4i=i3=−i i^{-4321}=\frac{1}{i^{4321}}=\frac{1}{i\cdot i^{4320}} = \frac{1}{i}=\frac{i^4}{i}=i^3=-i 。

例題1.3-6. 求 1+i3−i\frac{1+i}{\sqrt{3}-i} 的極座標表示式。

Geogebra 3: 極座標下的複數乘法運算

https://www.geogebra.org/m/fq6f9nby

Geogebra 4: 複數的極座標下的除法運算

https://www.geogebra.org/m/aaxguhhv

絕對值與共軛複數的性質

複數 a−bia-bi 稱為複數 z=a+biz=a+bi 的共軛複數，記作 z‾\overline z ，顯然 zz 和 z‾\overline z 對於實數軸對稱，即 z‾\overline z 為 z z 對於實數軸的鏡射(reflection)，顯然

arg⁡z‾=−arg⁡z\begin{equation} \arg\overline z=-\arg z \tag{1.3-14} \end{equation}
∣z∣2=z⋅z‾\begin{equation} \left|z\right|^2=z\cdot\overline z \tag{1.3-15} \end{equation}
∣z‾∣=∣z∣\begin{equation} \left|\overline z\right|=\left|z \right| \tag{1.3-16} \end{equation}

在複數平面上，三角不等式亦成立，我們有下列之結果：

定理1.3-2. (三角不等式) 若 z1,z2∈Cz_1,z_2 \in \Complex，則

∣z1+z2∣≤∣z1∣+∣z2∣\begin{equation} \left|z_1+z_2\right|\le\left|z_1\right|+\left|z_2\right| \tag{1.3-17} \end{equation}

等號成立之充要條件為

arg⁡z1=arg⁡z2\begin{equation} \arg z_1=\arg z_2 \tag{1.3-18} \end{equation}

又由 ∣z1∣=∣z1−z2+z2∣\left|z_1\right|=\left|z_1-z_2+z_2\right| 與三角不等式可得

∣z1∣=∣(z1−z2)+z2∣≤∣z1−z2∣+∣z2∣|z_1|=|(z_1-z_2)+z_2|\le |z_1-z_2|+|z_2|

或

∣z1∣−∣z2∣≤∣z1−z2∣|z_1|-|z_2|\le\left|z_1-z_2\right|

同理可得 ∣z2∣−∣z1∣≤∣z1−z2∣\left|z_2\right|-\left|z_1\right| \le \left|z_1-z_2\right|，所以下面不等式成立：

∣∣z1∣−∣z2∣∣≤∣z1−z2∣.\left|\left|z_1\right|-\left|z_2\right|\right| \le \left|z_1-z_2\right|.

性質： ∣z∣|z| 之性質如下：

  1. ∣z∣=0  ⟺  z=0=(0,0)|z|=0 \iff z=0=(0,0)，
  1. ∣z1⋅z2∣=∣z1∣⋅∣z2∣|z_1 \cdot z_2|=|z_1| \cdot |z_2|，
  1. ∣z1z2∣=∣z1∣∣z2∣\left| \frac{z_1}{z_2} \right| = \frac{|z_1|}{|z_2|} 。
  1. ∣∣z1∣−∣z2∣∣≤∣z1−z2∣≤∣z1∣+∣z2∣.\left|\left|z_1\right|-\left|z_2\right|\right| \le \left|z_1-z_2\right|\le |z_1|+|z_2|.

[證明] 自行練習。

例題1.3-7. 請說明下列關係所呈現的集合型式：

  1. ∣z−1∣=Re(z)+1|z-1|=\text{Re}(z)+1，
  1. ∣z+2∣=∣z−1∣|z+2|=|z-1|，
  1. ∣z−i∣<2|z-i|<2，
  1. ∣z−1∣+∣z+1∣=7|z-1|+|z+1|=7。

習題
  1. Sketch the sets of points determined by the following relations.

    (a) ∣z+1−2i∣=2|z+1-2i|=2.

    (b) Re(z+1)=0\text{Re}(z+1)=0.

    (c) ∣z+2i∣≤1|z+2i| \leq 1.

    (d) Im(z−2i)≥6\text{Im}(z-2i) \geq 6.

  1. Prove that 2∣z∣≥∣Re(z)∣+∣Im(z)∣\sqrt{2}|z| \geq |\text{Re}(z)|+|\text{Im}(z)|.

17. Suppose that either ∣z∣=1|z|=1 or ∣w∣=1|w|=1. Prove that ∣z−w∣=∣1−z‾w∣|z-w|=|1-\overline{z}w|.

  1. 求使得 Arg1z=−Argz\mathrm{Arg}\frac{1}{z}=-\mathrm{Arg}z 不成立的 zz。
  1. 練習證明 arg⁡1z=−arg⁡z\arg\frac{1}{z}=-\arg z 。