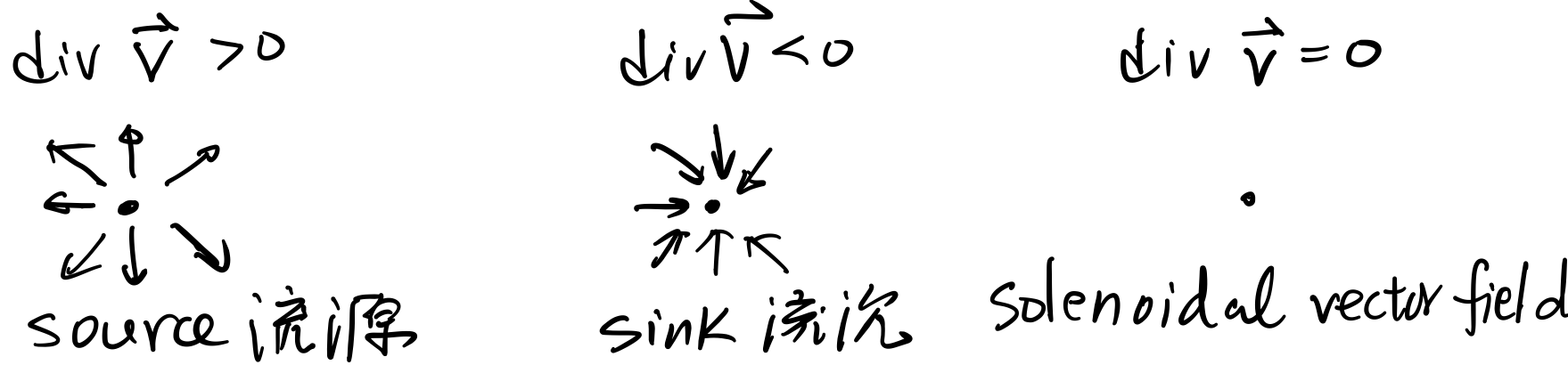補充：向量場與圓柱位勢能 (Vector Field and Cylindrical Potentials)

向量場(Vector Field)

先考慮液體流場(flow field)，假設其速度向量為 V⃗=(P,Q)\vec{V}=(P,Q)，其中P,QP, Q 為平面域 DD 上的

一階導數連續函數(i.e., P,Q∈C(D)P,Q\in C(D))。若以向量 i⃗\vec{i}, j⃗\vec{j}, k⃗\vec{k} 分別表示卡氏座標沿著x, y, zx,~y,~z-軸之單位向量，則有

V⃗=Pi⃗+Qj⃗.\vec{V}=P\vec{i}+Q\vec{j}.

若令算子 ∇\nabla (讀成del) 為

∇=(∂∂x,∂∂y)=i⃗∂∂x+j⃗∂∂y\nabla=\left(\frac{\partial}{\partial x},\frac{\partial}{\partial y}\right)=\vec{i}\frac{\partial}{\partial x}+\vec{j}\frac{\partial}{\partial y}

則微積分介紹過的散度 (divergence) divV⃗\text{div} \vec{V} 與旋度 (curl) curl V⃗\text{curl}~\vec{V} 為

divV⃗=∇⋅V⃗=∂P∂x+∂Q∂y=Px+QycurlV⃗=∇×V⃗=∣i⃗j⃗k⃗∂∂x∂∂y∂∂zPQ0∣=k⃗(∂Q∂x−∂P∂y)=k⃗(Qx−Py)\begin{align*} \text{div}\vec{V} &=\nabla \cdot \vec{V} = \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}=P_x+Q_y\\ \text{curl}\vec{V} &=\nabla \times \vec{V} =\begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ \frac{\partial}{\partial x} &\frac{\partial}{\partial y}& \frac{\partial}{\partial z} \\ P & Q & 0 \end{vmatrix}=\vec{k} \left( \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)=\vec{k} ( Q_x-P_y) \end{align*}

試問這兩個量物理意義為何？以及與調和函數或解析函數之關係為何？可以透過流場來說明。

divV⃗\text{div} \vec{V} 之物理意義

先討論 divV⃗\text{div} \vec{V} 之物理意義。考量下列流場：

圖片取自https://tylerxhobbs.com/works/2018/unfenced-existence

於其內定義一塊長寬為 Δx,Δy\Delta x, \Delta y 之控制體積 (control volume)，右下較之座標為(x0,y0)(x_0,y_0)。想要了解進入此控制體積流體質量之變化，參考下圖：

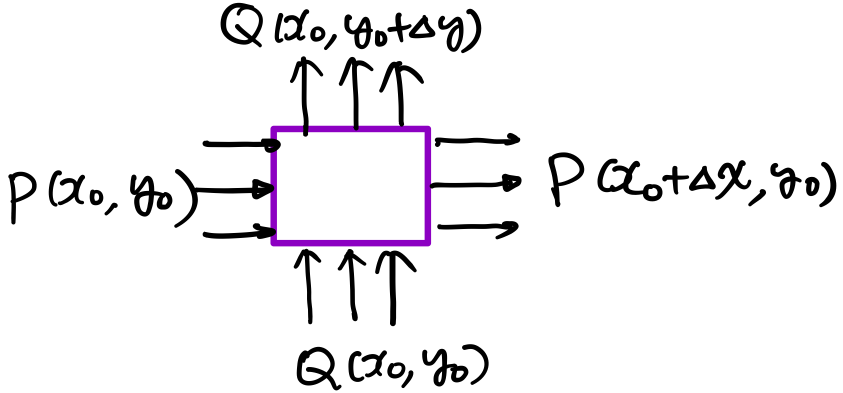
其中假設水平線上的Q是相同以及垂直線上的P是相同。如此一來，水平方向之淨流入量為

[P(x0+Δx,y0)−P(x0,y0)]Δy≈∂P∂x(x0,y0)ΔxΔy,[P(x_0+\Delta x, y_0)-P(x_0,y_0)]\Delta y\approx \frac{\partial P}{\partial x}(x_0,y_0) \Delta x \Delta y,

垂直方向之淨流入量為

[Q(x0,y0+Δy)−Q(x0,y0)]Δx≈∂Q∂y(x0,y0)ΔxΔy,[Q(x_0,y_0+\Delta y)-Q(x_0,y_0)]\Delta x\approx \frac{\partial Q}{\partial y}(x_0,y_0) \Delta x \Delta y,

因此控制體積之單位面積淨流量為

淨流入量ΔxΔy≈∂P∂y(x0,y0)+∂Q∂y(x0,y0)=div V⃗(x0,y0).\frac{\text{淨流入量}}{\Delta x\Delta y}\approx \frac{\partial P}{\partial y}(x_0,y_0)+\frac{\partial Q}{\partial y}(x_0,y_0)=\text{div}~\vec{V}(x_0,y_0).

因此 div V⃗\text{div}~\vec{V} 之大小表示此點是單位面積流通增量

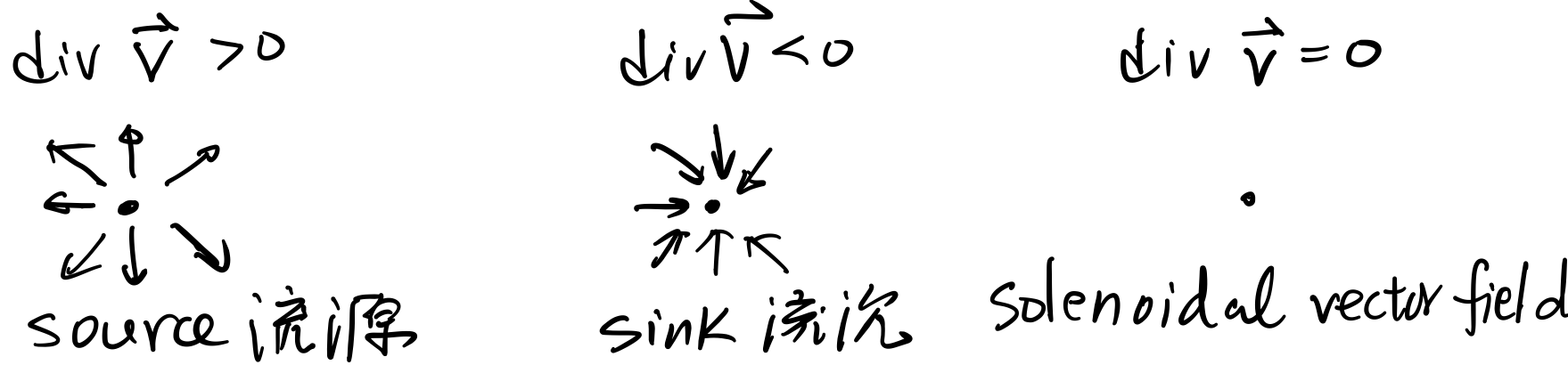
故 div V⃗(x,y)=0, ∀(x,y)∈D\text{div}~\vec{V}(x,y)=0,~\forall(x,y)\in D，則表示域 DD 內之質量守恆(conservation of mass)。

curl V⃗\text{curl}~\vec{V}之物理意義

接著討論 curl V⃗\text{curl}~\vec{V} 之物理意義。在下列流場：

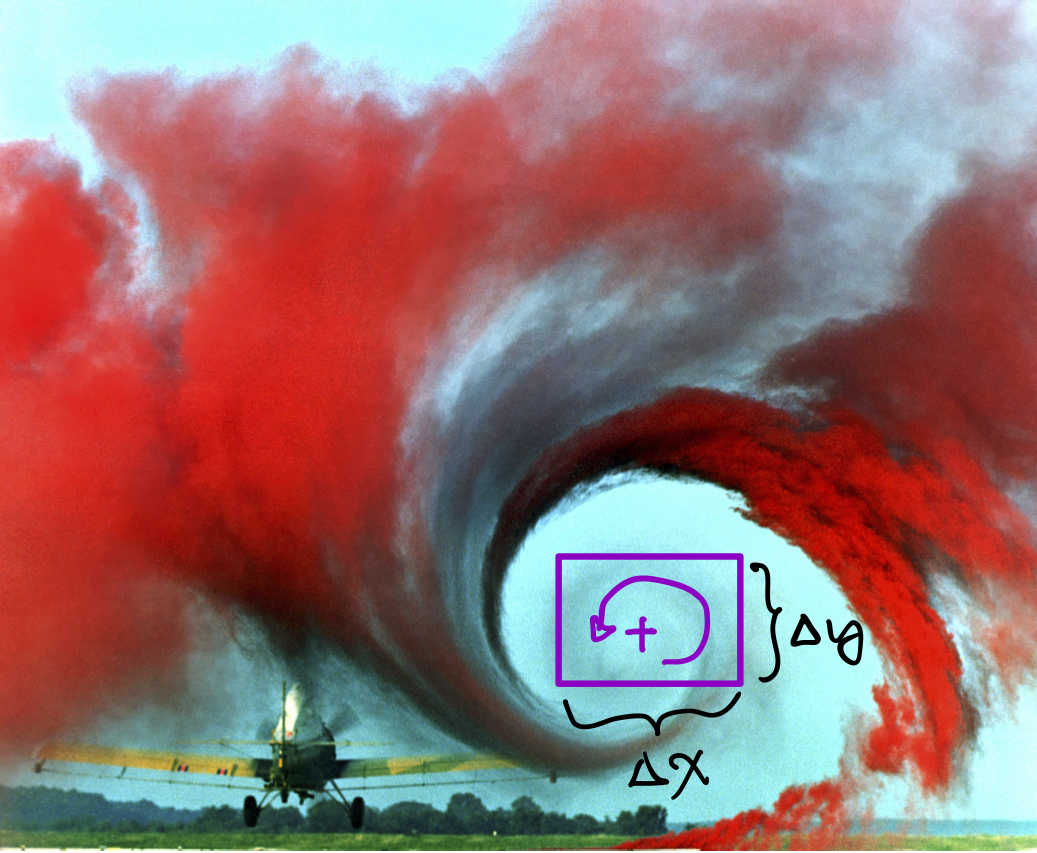
圖形網址：https://upload.wikimedia.org/wikipedia/commons/f/fe/Airplane_vortex_edit.jpg

控制體積邊長亦為 Δx\Delta x 與 Δy\Delta y，其左下角的座標為 (x0,y0)(x_0, y_0)，考量下列簡圖：

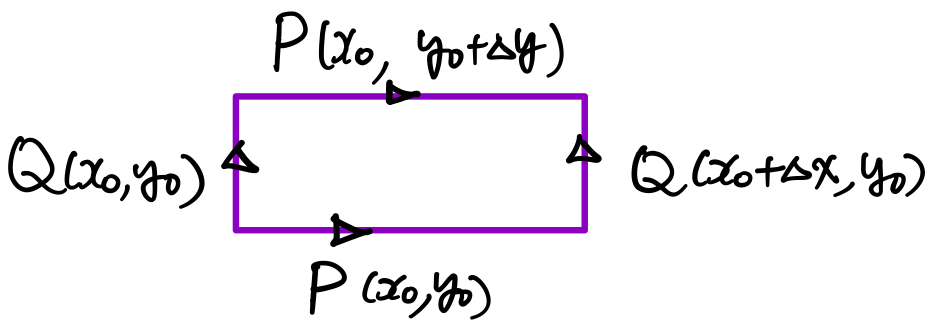
沿此控制體積邊界之旋流量為

P(x0,y0)Δx+Q(x0+Δx,y0)Δy−P(x0,y0+Δy)Δx+Q(x0,y0)Δy=[Q(x0+Δx,y0)−Q(x0,y0)]Δy−[P(x0,y0+Δy)−P(x0,y0)]Δx≈∂Q∂x(x0,y0)ΔxΔy−∂P∂x(x0,y0)ΔyΔx\begin{align*} &P(x_0,y_0)\Delta x+Q(x_0+\Delta x,y_0)\Delta y-P(x_0,y_0+\Delta y)\Delta x+Q(x_0,y_0)\Delta y \\ &= [Q(x_0+\Delta x,y_0)-Q(x_0,y_0)]\Delta y -[P(x_0, y_0+\Delta y)-P(x_0,y_0)]\Delta x \\ &\approx \frac{\partial Q}{\partial x}(x_0,y_0)\Delta x \Delta y -\frac{\partial P}{\partial x}(x_0,y_0)\Delta y \Delta x \end{align*}

因此控制體積之單位面積淨旋流量為

總旋流量ΔxΔy≈∂Q∂x(x0,y0)−∂P∂y(x0,y0)=curl V⃗(x0,y0).\frac{\text{總旋流量}}{\Delta x\Delta y}\approx \frac{\partial Q}{\partial x}(x_0,y_0)-\frac{\partial P}{\partial y}(x_0,y_0)=\text{curl}~\vec{V}(x_0,y_0).

故 curl V⃗\text{curl}~\vec{V} 之大小表示此點是單位面積旋流增量，即

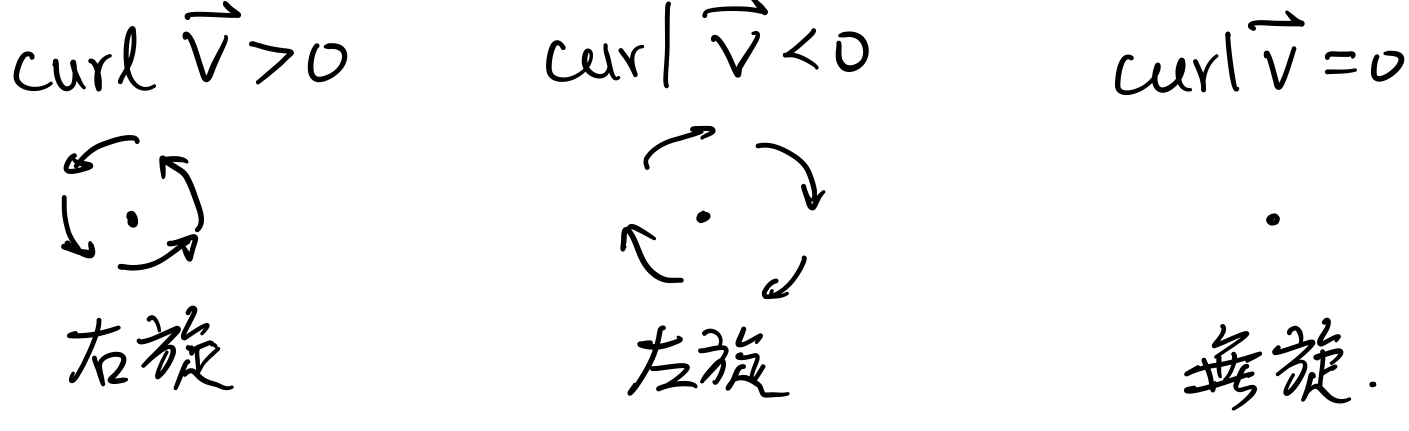
即當 curl V⃗(x,y)=0, ∀(x,y)∈D\text{curl}~\vec{V}(x,y)=0,~\forall(x,y)\in D，則表示域 DD 內為無旋流(irrotational flow)。

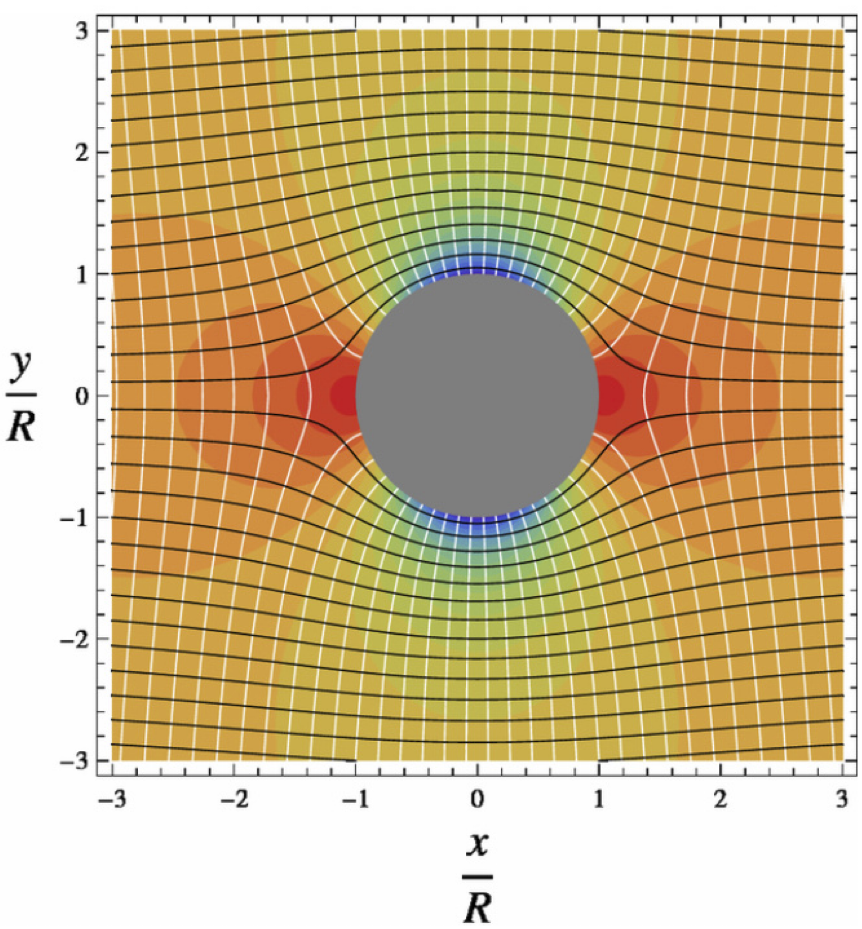
圓柱位勢能(Potential flow around a circular cylinder)

以下說明，參考 Wiki 網頁 https://en.wikipedia.org/wiki/Potential_flow_around_a_circular_cylinder

考量針對無黏滯 (inviscid)、不可壓縮 (incompressilbe)與無旋流場，場中有放置一RR圓柱，對應之流場圖示如下：

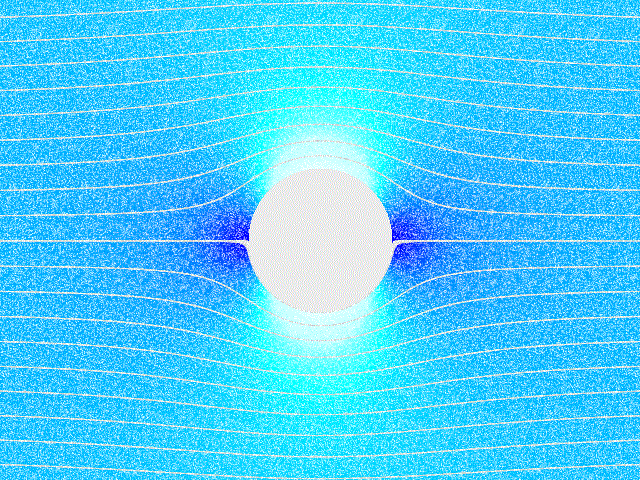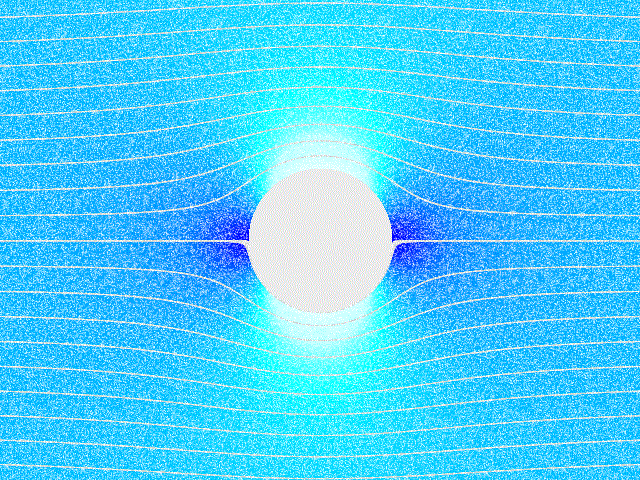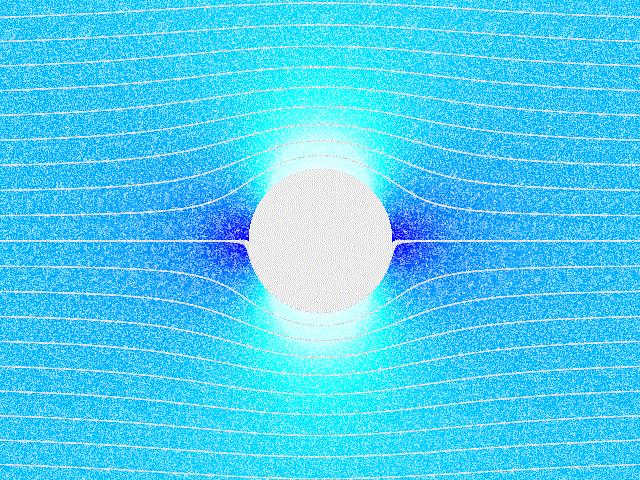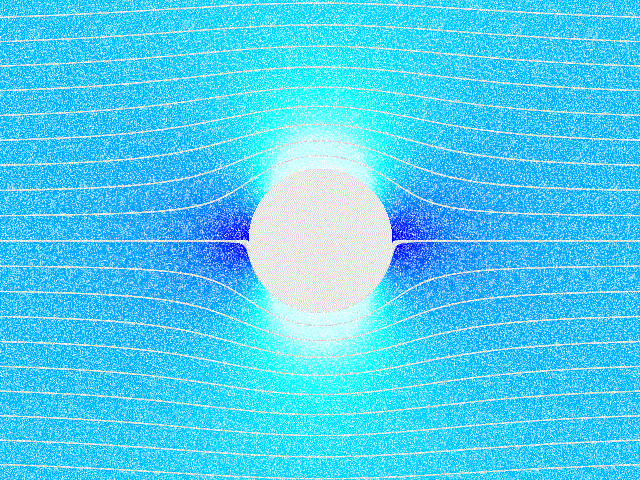
設速度場為V⃗\vec{V}並以 DD 表示流場的域，對應的座標與進入流場的流體速度為 V⃗=(U∞,0)\vec{V}=(U_\infty,0)：

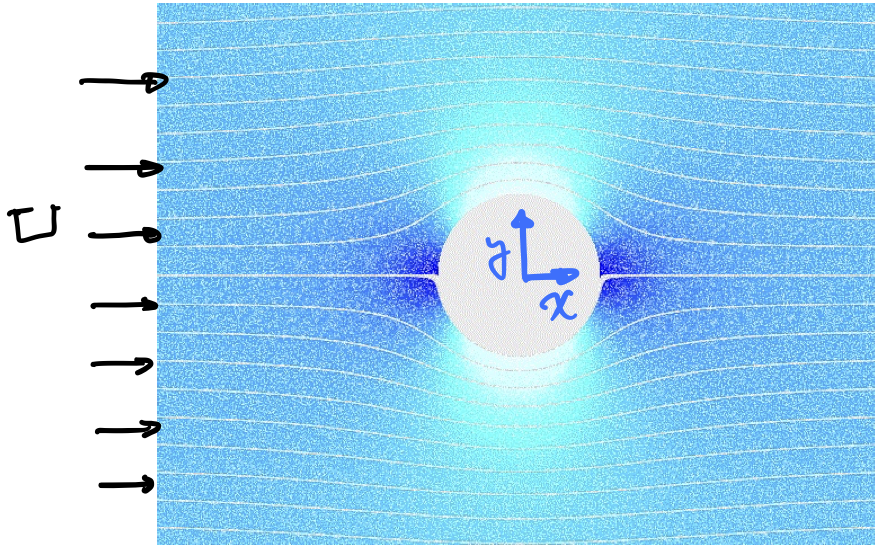
則∇⋅V⃗=0\nabla\cdot \vec{V}=0 以及 ∇×V⃗=0\nabla \times \vec{V}=0，由定理3.3-3知∃ϕ∈H(D) \exists \phi\in H(D) 使得 V⃗(x,y)=∇ϕ(x,y)\vec{V}(x,y) = \nabla\phi(x,y)，由於 ϕ\phi 為調和函數，因此

Δ2ϕ(x,y)=0,∀(x,y)∈D.\Delta^2\phi(x,y)=0,\quad \forall (x,y)\in D.

取極座標表示，則

V⃗=(U(r,θ),V(r,θ))=∇ϕ=(∂ϕ∂x,1r∂ϕ∂θ).\vec{V}=(U(r,\theta), V(r,\theta))=\nabla \phi=\left(\frac{\partial \phi}{\partial x},\frac1{r}\frac{\partial \phi}{\partial \theta}\right).

以及

Δ2ϕ(r,θ)=∂2ϕ∂r2+1r∂ϕ∂r+∂2ϕr2∂θ2=1r∂∂r(r∂ϕ∂r)+∂2ϕr2∂θ2=0\Delta^2 \phi(r,\theta) =\frac{\partial^2 \phi}{\partial r^2}+\frac1{r}\frac{\partial \phi}{\partial r}+\frac{\partial^2 \phi}{r^2\partial \theta^2} =\frac1{r}\frac{\partial}{\partial r}\left( r\frac{\partial \phi}{\partial r}\right)+\frac{\partial^2 \phi}{r^2\partial \theta^2} =0

代入邊界條件

{r=R時,ϕr(R,θ)=0r≫R時,V⃗(R,θ)=U∞+i⋅0=U∞.\begin{cases} r=R\text{時}, &\phi_r(R,\theta)=0\\ r\gg R\text{時}, &\vec{V}(R,\theta)=U_\infty+i\cdot 0 = U_\infty.\\ \end{cases}

透過分離變數法，解 Laplace 方程式，可得

ϕ(r,θ)=U∞r(1+R2r2)cos⁡θ\phi(r,\theta)=U_\infty r \left(1+\frac{R^2}{r^2}\right)\cos\theta

即

V⃗=(U(r,θ),V(r,θ)=U∞r(1+R2r2)(cos⁡θ,−sin⁡θ).\vec{V}=(U(r,\theta),V(r,\theta)=U_\infty r\left(1+\frac{R^2}{r^2}\right)(\cos\theta,-\sin\theta).

此外，對應的正交曲面 ψ\psi 則為

ψ(r,θ)=U∞r(1−R2r2)sin⁡θ.\psi(r,\theta)=U_\infty r \left(1-\frac{R^2}{r^2}\right)\sin\theta.

流場的等高線圖如下，其中白線表示 ϕ\phi (位勢能函數)、黑線為 ψ\psi (流線函數)：

圖形網址：https://upload.wikimedia.org/wikipedia/commons/1/17/CylinderVelocityPressure.png